Dois blocos e , um sobre o outro, deslocam-se rampa abaixo com uma força aplicada sobre o bloco . Os blocos movem-se conjuntamente a velocidade constante de . O coeficiente de atrito cinético entre o bloco e a rampa é , e o coeficiente de atrito estático entre os blocos é . A rampa faz com a superfície horizontal. O bloco da figura pesa e o bloco pesa .
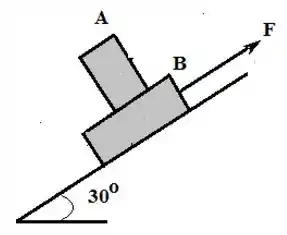
Desenhe dois diagramas do corpo livre separados mostrando as forças que atuam sobre e sobre .
Determine a força necessária para que os blocos apresentem o movimento descrito.
Quais são as intensidades e o sentido da força de atrito no bloco ?
Passo 1
Para o D.C.L dos blocos, temos:
Bloco :
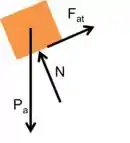
Bloco:
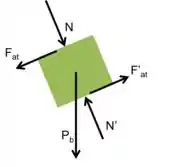
Passo 2
Para determinar a força , vamos montar as equações de movimento para os dois blocos, como os blocos se movem com velocidade constante, a força resultante em ambos é nula. Para o bloco , analisando somente o movimento em , ou seja, ao longo da rampa, temos:
Para o bloco :
Substituindo o valor da , temos:
Substituindo, temos:
Passo 3
No bloco , temso que a força de atrito vale:
Resposta
Ver figuras.