Dois blocos de massas e estão ligados por um fio ideal que passa por uma polia ideal fixa numa parede. Os coeficientes de atrito estático e cinético entre os blocos valem e , respectivamente, e os coeficientes de atrito estático e cinético entre a massa e o solo valem e . Se a aceleração relativa entre os blocos é de , o valor do módulo da força horizontal aplicada a é:
Passo 1
Pra gente achar o valor da força F vamos usar a segunda lei de newton em cada corpo. Pra isso, precisamos fazer o diagrama de forças para os dois blocos.
Já vamos fazer algumas observações. O módulo da tração vai ser o mesmo, já que o fio é sem massa.
O enunciado fala que a aceleração relativa entre os blocos é de . Mas notem que conforme a força F puxa o bloco M para a direita, por causa do fio que une os blocos, vamos ter o bloco m indo pra esquerda. Ou seja, a aceleração de cada um está para um sentido,logo, temos que os vetores acelereção de cada corpo estão em sentidos opostos, mas tem mesmo módulo .
Passo 2
Para o bloco de massa (vamos chamá-lo de bloco 1) temos o peso, a tração, a força Normal e temos também a força de atrito.
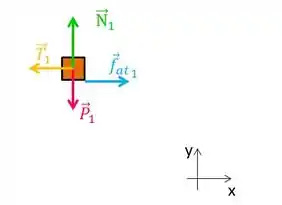
A segunda lei de newton é:
Na horizontal, temos que o movimento é para a aesquerda, então a resultante vale:
Na vertical, não há movimento, ou seja, não há aceleração, então:
Beleza! Sabemos que
Como há movimento e como estamos analisando o bloco 1, temos que:
Substituindo os valores:
Usando que , com vimos no passo anterior, podemo calcular :
Beleza!!
Agora, vamos fazer a mesma coisa para o bloco M (que vamos chamar de bloco 2).
Passo 3
Para o bloco 2 temos o peso, a tração, a força Normal e temos também a força de atrito com o chão, a reação da força de atrito com o bloco 1, a reação da normal de 1 e também a força F.
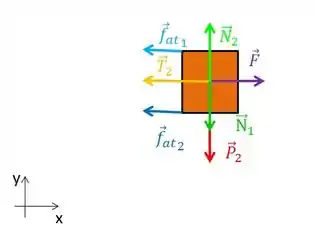
Pela segunda lei de newton, temos:
Na direção vertical:
Na direção horizontal:
Como falamos antes,
A vai ser . Substituindo:
Mas temos que:
Então:
Agora, é só substituir tudo na equação que tem o F:
Uhuul! Essa é a nossa resposta!