Uma caixa está em repouso sobre uma superfície horizontal áspera. Os coeficientes de atrito estático e cinético entre a caixa e a superfície são µe = 0,40 e µc = 0,20, respectivamente.
(a) Para pôr a caixa em movimento horizontal com a menor força aplicada possível, a força aplicada deve ser horizontal, fazer um ângulo abaixo da horizontal ou um ângulo acima da horizontal? Justifique qualitativamente sua resposta.
(b) Se o peso da caixa é 50 N e a força aplicada faz um ângulo de 30° acima da horizontal, determine a intensidade mínima da força aplicada capaz de pôr a caixa em movimento horizontal.
(c) Nas condições do item anterior, supondo que a força externa mínima que dá início ao movimento horizontal é atingida e mantida, a caixa se moverá com velocidade constante ou aceleração constante? Justifique a resposta.
Passo 1
Vamos começar analisando o diagrama de corpo livre para a força horizontal aplicada.
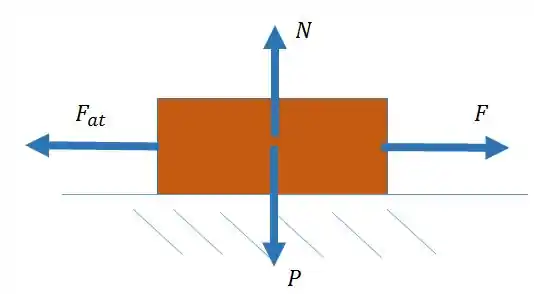
Nesse caso,
E a força aplicada mínima necessária para pôr a caixa em movimento tem módulo:
Passo 2
Agora se analisarmos com uma força inclinada para cima da horizontal:
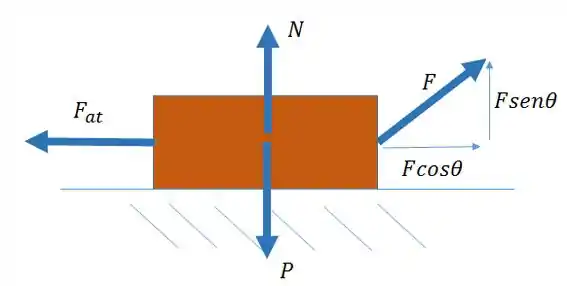
Nesse caso, a normal não seria igual ao peso:
Como a normal seria menor, a força de atrito máxima também seria menor e a força mínima necessária seria:
Assim, uma força menos intensa do que no caso de aplicação horizontal pode pôr a caixa em movimento.
Repare que se a inclinação fosse para baixo, o efeito seria contrário, já que teríamos uma normal ainda maior, o que aumentaria a força mínima necessária,
Passo 3
No item B, podemos usar o diagrama de corpo livre feito no passo anterior:
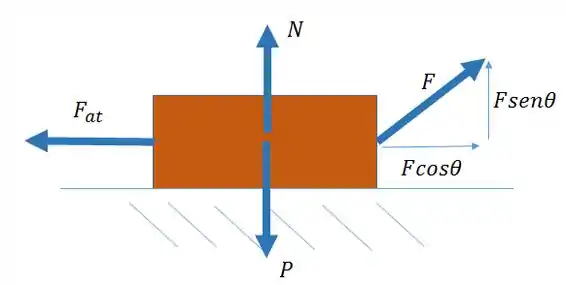
Sabemos que na situação da caixa estar na iminência de deslizar:
Temos que e que
Combinando estas equações podemos obter:
Ajeitando essa parada aí:
Substituindo por :
Passo 4
O item C pergunta o que acontece com a velocidade e com a aceleração, depois que o movimento horizontal é começado.
Vamos entender o que acontece:
A partir do instante em que a intensidade da força aplicada torna-se igual à da força de atrito estático máxima, a caixa entra em movimento e passa a atuar a força de atrito cinético, que é menor do que a força de atrito estático máxima.
Portanto, haverá uma força resultante na direção x. Isso é visível porque a força mínima necessária será maior do que a força de atrito cinético (o coeficiente de atrito cinético é menor).
Tendo uma força resultante, pela segunda lei de Newton, podemos concluir que haverá também aceleração.
Logo, a velocidade não será constante.
Resposta
- Fazer um ângulo acima da horizontal
- Aceleração constante