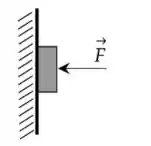
5) Uma força , de módulo 12 N, pressiona um bloco de massa m = 0,5 Kg contra uma parede vertical, como mostra a figura. O coeficiente de atrito estático entre a parede e o bloco é e o cinético é . Utilize, neste problema, para o módulo da aceleração da gravidade. Sobre esta situação, é correto afirmar que
(a) a força total que a parede exerce sobre o bloco tem módulo 13 N e o bloco não escorrega.
(b) a força total que a parede exerce sobre o bloco tem módulo 17 N e o bloco não escorrega.
(c) a força total que a parede exerce sobre o bloco tem módulo 12 N e o bloco não escorrega.
(d) a força total que a parede exerce sobre o bloco tem módulo 5 N e o bloco escorrega.
(e) a força total que a parede exerce sobre o bloco tem módulo 5 N e o bloco não escorrega.
Passo 1
Fala aí, galerinha!! Aqui a gente tem um problema de aplicação das leis de Newton. Naquela figura ali nós temos um bloco onde uma força é aplicada. Entre o bloco e aparece existe um atrito, certo? Então a gente tem essas forças aqui atuando no bloco:
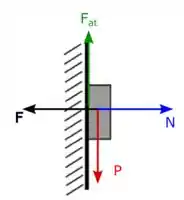
Onde é a força normal que a parede exerce no bloco, é a força peso e é a força de atrito. Show! Se a gente olhar as afirmações que estão aparecendo para a gente, todas elas falam sobre o bloco escorregar ou não e sobre a força total que a parede exerce no bloco, que é a força normal somada com a força de atrito (a soma é vetorial, hein)!
Então, o que a gente vai fazer aqui, é calcular a força normal e calcular a força de atrito estático máxima que a parede consegue fazer no bloco através de:
Olha só, a gente usa a força de atrito estático aqui pois ela quem vai ser responsável por deixar ou não o bloco escorregar. Beleza?
Então vamos usar essas informações para resolver essa. Partiiiu!!
Passo 2
Vamos começar calculando a força normal que a parede exerce no bloco. Pelo diagrama que a gente desenhou e adotando que o sentido para a direita é positivo e como o bloco não se move nessa direção, podemos escrever que:
Uma vez que a gente tem a força normal, podemos ver quanto vale o módulo da força de atrito estático usando a expressão:
Beleza!
Passo 3
Agora a gente tem que ver se o bloco escorrega ou não. Olhando o diagrama de forças: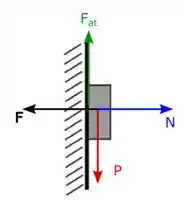
Percebemos que as forças que existem na direção vertical (a direção que o bloco pode escorregar) são o peso e a força de atrito. Na condição em que o bloco não se move, temos:
Onde é a força de atrito estático e adotamos o sentido para cima como o sentido positivo.
Agora a nossa tarefa é ver se essa condição é satisfeita. É importante a gente lembrar que a condição é a condição máxima de equilíbrio. Qualquer valor de menor que a força de atrito que a gente calculou garante que o bloco não desce, ok?
O peso do bloco é dado por:
Usando e temos:
Dessa forma temos
E então o bloco não desliza!
Passo 4
Por enquanto só conseguimos descobrir que o bloco não escorrega e isso já elimina algumas de nossas opções 😊
Mas precisamos calcular agora a força total que a parede exerce no bloco. Em nosso diagrama a gente percebe que a força total vai ser dada pela soma vetorial entre a força normal e a força de atrito estático . O módulo da força total é dado por:
Então encontramos a resposta desse problema 😊 Vamos para o próximo??
Resposta
(a) a força total que a parede exerce sobre o bloco tem módulo 13 N e o bloco não escorrega.