Considere W o subespaço do gerado por , , e . Isto é, W=[
i. O vetor (2,-3,2,2) pertence a W?
ii. Determine uma base para W e sua dimensão.
iii. W=? Justifique.
Passo 1
i. Para que o vetor (2,-3,2,2) pertença a W, ele deve ser escrito como combinação linear dos vetores que geram esse subespaço.
Ou seja, devem existir a, b, c e d tais que:
Vamos tentar achar esses valores. Resolvendo:
Somando as duas primeiras equações:
Substituindo esse valor de a na segunda equação, vamos encontrar:
Agora substituindo c na terceira equação:
Portanto, quaisquer valores de a,b, c e d que satisfazem:
Irão gerar o vetor (2,-3,2,2). Logo, ele pertence a W.
Passo 2
ii. Sabemos que a base de um subespaço vetorial é um conjunto linearmente independente de vetores capaz de gerar todo esse subespaço.
O enunciado deu pra gente que W era gerado por , , e .
Vamos ver se esses quatro vetores são LI.
Pra isso, vamos coloca-los nas linhas de uma matriz e escalonar, beleza?




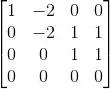
Ih, a quarta linha zerou!!
Significa que o vetor que tava lá, o , é uma combinação linear dos outros.
Então se tirarmos ele do conjunto formado pelos 4 vetores, vamos ter um conjunto LI e esse conjunto LI gera todo nosso subespaço W.
Então uma base pra W vai ser:
Como temos 3 vetores nesse conjunto:
Passo 3
iii. Temos:
E vimos que:
Logo,
Ou seja, com os vetores de W, não conseguimos gerar todo o (para gerar precisaríamos de 4 vetores LI, mas só temos 3)
Resposta
i. Sim
ii.
iii.