Exercícios Resolvidos de Energia Interna de um gás e Calores Específicos Molares
Ver TeoriaEnunciado
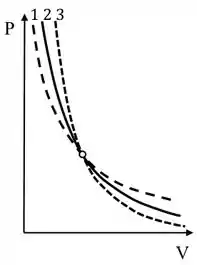
A figura ao lado mostra um diagrama PV, no qual estão assinaladas 3 curvas possíveis que passam por um mesmo ponto (representado pelo círculo). Uma dessas curvas representa uma transformação isotérmica de um gás ideal, e as outras duas transformações adiabáticas, sendo uma delas a curva adiabática seguida por um gás ideal monoatômico, e a outra a seguida por um gás ideal diatômico. Sendo 1 = curva tracejada; 2 = curva cheia; 3 =
curva tracejada fina, identifique qual curva corresponde a qual processo.
Passo 1
O que diferencia as três curvas são as inclinações (derivadas), sendo a curva 3 a que decai mais rapidamente (mais inclinada), seguida da 2 e a 1, respectivamente.
Mas como relacionar a inclinação com os processos isotérmicos e adiabáticos?
Primeiro, vamos lembrar que num processo isotérmico, a relação entre a pressão e volume vem do “pi-vi-ti po-vo-to”, onde pode-se cortar a temperatura:
Então, no diagrama PV teremos algo do tipo
Já no processo adiabático, a relação é
Passo 2
Como , então a curva adiabática decai mais rapidamente do que a isotérmica.
Podemos concluir que a isotérmica é a menos inclinada, no caso, a curva 1.
Passo 3
No caso das duas adiabáticas, precisamos lembrar quem é o para o caso monoatômico e para o diatômico.
Tal dado é fornecido no formulário que acompanha a prova, caso você não lembre de cabeça.
Como , a curva 3, mais inclinada, é adiabática monoatômica.
A curva 2, adiabática diatômica.
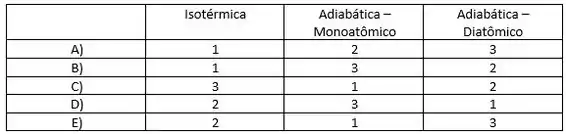
Resposta
B) Isotérmica-1, Adiabática Monoatômica-3, Adiabática Diatômica-2