Exercícios Resolvidos de Energia Interna de um gás e Calores Específicos Molares
Ver TeoriaEnunciado
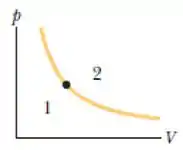
O ponto na figura representa o estado inicial de um gás ideal e a isoterma que passa pelo ponto divide o diagrama p-V nas regiões 1 e 2. Assinale a alternativa correta a respeito da variação da energia interna ΔEint nos seguintes processos:
a) ΔEint é negativa se o estado do sistema se move para qualquer ponto da região 1 e ΔEint é positiva se o estado do sistema se move para qualquer ponto da região 2;
b) ΔEint é positiva se o estado do sistema se move para qualquer ponto da região 1 e ΔEint é negativa se o estado do sistema se move para qualquer ponto da região 2;
c) ΔEint é negativa se o estado do sistema se move para baixo na curva isoterma;
d) ΔEint é positiva se o estado do sistema se move para baixo na curva isoterma;
e) ΔEint é nula se o estado do sistema se move para qualquer ponto da região 1 ou da região 2;
Passo 1
Pra fazer essa questão, tem umas coisas que você precisa lembrar sobre isotermas.
Uma isoterma divide um diagrama p-V em duas regiões. A região 2 tem temperaturas maiores que a da isoterma, e a região 1 tem temperaturas menores que a da isoterma.
Ao longo da isoterma a temperatura não muda! Beleza?
Vamos lembrar agora da fórmula da variação da energia interna:
Então se a variação de temperatura é negativa a variação de energia interna também é. Idem pra quando for positiva!
Passo 2
Vamos analisar as afirmativas.
a) Quando o sistema se move pra um ponto da região 1, a variação de temperatura é negativa. Então a variação de energia interna também é. Quando o sistema se move pra um ponto da região 2, a variação de temperatura é positiva. Então a variação de energia interna é positiva. Verdadeira!
b) Vimos na letra a que é ao contrário. Falsiane!
c) Quando o sistema se move na curva, não tem variação de temperatura nem de energia interna. Então essa é falsa.
d) Falsa, pelo mesmo motivo da letra c.
e) A variação de energia interna só é nula se o sistema se move em cima da isoterma. Falsa!
Resposta
Letra A.