Um mol de um gás ideal monoatômico pode atingir o mesmo estado final através de três processos distintos como mostrado no gráfico abaixo.
Dados e .
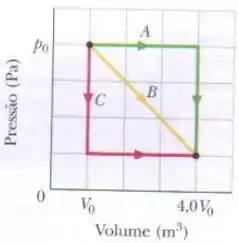
A variação de energia térmica no processo A é:
A) 0 J
B) -3,0 J
C) -37,5 J
D) 37,5 J
E) 24,9 J
Passo 1
Precisamos lembrar que a energia térmica (energia interna) é uma função de estado. Sua variação só depende do ponto final e do ponto inicial.
Vamos calcular a temperatura no ponto final usando “pi-vi-ti po-vo-to”:
Passo 2
Pelo gráfico, volume final é . No eixo vertical, como temos quatro divisórias até o , então cada divisória equivale a , pressão final é .
Concluimos que !
Se a temperatura não varia, então a energia térmica também não varia.
Resposta
A) 0 J