Determine o valor de
Passo 1
OPAAA!! Queremos calcular o , certo?! Lembra que a função é uma função periódica? Ela vai se repetir depois do ou , lembra?

Então vamos quebrar o em duas parcelas para facilitar a nossa vida!! Vem comigo!
Passo 2
Vamos fazer o seguinte. Como a função é periódica
Sabemos que , basta olhar para o círculo trigonométrico:
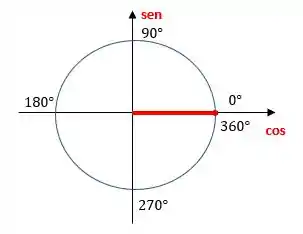
Beleza?!
Assim,
Passo 3
Para encontrar o valor de basta olharmos pra tabelinha com o valor dos principais ângulos
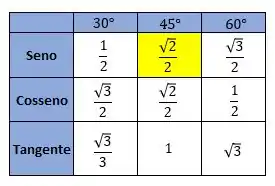
Portanto,
Show de bola?!?!