19. Qual item melhor representa o gráfico da função
Observação: As linhas pontilhadas representam uma escala de uma unidade na vertical e unidades na horizontal.
Passo 1
Oi, galerinha! Tudo bom? Aqui precisamos dizer qual gráfico representa a seguinte função:
Para isso, é importante lembrarmos com a cara de uma função
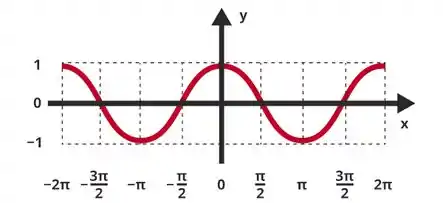
Repara que o valor da função é máximo (igual a ) para quando o cosseno é zero ou , onde é um número inteiro ímpar. Além disso, ela terá valores mínimos (igual a ) em . E terá valor nulo em .
Então a dica aqui é avaliar esses pontos e ver quais que se encaixam no gráfico.
Passo 2
Vamos começar pelo ponto de máximo do cosseno! A parte terá valor máximo quando o que tiver dentro do nosso cosseno for zero. Ou seja, vamos ver quanto vale,
Logo, a nossa função cosseno terá um máximo em .
Agora vamos calcular a nossa nesse ponto,
Opaaa! Então temos o nosso primeiro ponto! Temos que buscar um gráfico que tenha um ponto .
Passo 3
Analisando os gráfico, podemos perceber que apenas um deles apresenta o ponto
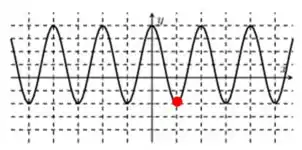
Lembrando que as linhas pontilhadas representam uma escala de uma unidade na vertical e unidades na horizontal.
Prontinho!