Determine o período das seguintes funções:
Passo 1
O período () de uma função é o intervalo que ela demora em se repetir. Olhando para o gráfico da função cosseno, podemos ver que ela se repete no intervalo de até .
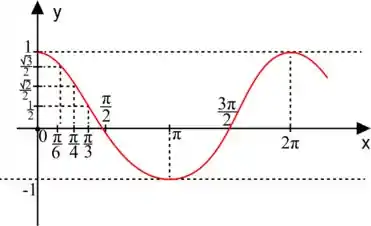
Então, o período da função cosseno é sempre .
Passo 2
-
O período do cosseno é sempre , então toda vez que variar em , teremos a função se repetindo. Isso é a mesma coisa que dizer que é igual a .
Então, agora igualamos seu argumento a esse valor:
Só isso mesmo!
Passo 2
Novamente, vamos chamar de e igualar seu argumento a esse valor:
Passo 3
c)
Aqui a gente segue os mesmos passos: o período do cosseno é sempre , então chamamos de e igualamos seu argumento a esse valor.
Mas, agora, CUIDADO! Neste caso, o indica somente que a função está deslocada unidades para a direita.
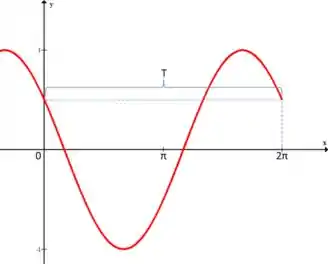
Portanto, o período não é afetado e será:
Passo 4
d)
Na soma de seno e cosseno, o período continua sendo e, portanto: