Um ponto A que se movimenta sobre uma circunferência, tem sua posição considerada na vertical, no instante descrita pela relação para . Nesse caso, a medida do diâmetro dessa circunferência é:
a) 30
b) 40
c) 50
d) 80
e) 120
Passo 1
Bom, ele deu a equação da posição vertical. Vamos ver o que conseguimos fazer com isso?
Lembra que a função seno pode assumir como valor máximo e como valor mínimo? Para quem não lembra, olha o gráfico dela ai embaixo,
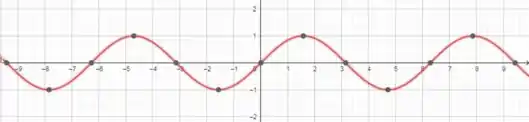
Vamos usar esse mesmo raciocínio para achar o nosso e . Lembra que nós temos essa função,
O valor máximo da posição vertical vai ser quando o seno for mínimo. Ou seja:
Do mesmo jeito, a posição vertical vai ser mínima quando o seno for máximo:
Passo 2
Beleza, mas o que podemos fazer com essa informação?
Esse ponto A que ele tá falando no enunciado tá se movimentando de acordo com uma função trigonométrica, assumindo valores sempre maiores que 80 e menores que 120. Mas sempre dentro desse intervalo.
E como a função é PERIÓDICA, ele fica repetindo esse movimento de vai-e-vem, descrevendo uma circunferência (como disse o enunciado).
Aí que vem o pulo do gato!

Vamos traçar uma linha horizontal onde temos o e e colocar uma circunferência entre essas linhas, pois a nossa função varia sempre dentre desse intervalo,
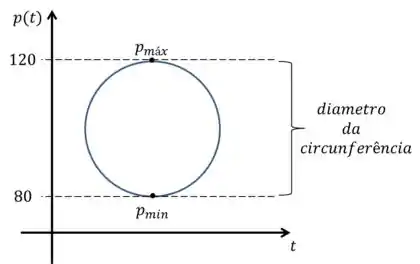
Repara que ao fazermos isso, a gente consegue identificar qual seria o diâmetro da circunferência. E o diâmetro vai ser dado pela diferença do ponto máximo para o ponto mínimo, ou seja:
Ou seja, . LETRA B
Resposta
Letra B