A figura mostra o gráfico da função f, dada pela lei
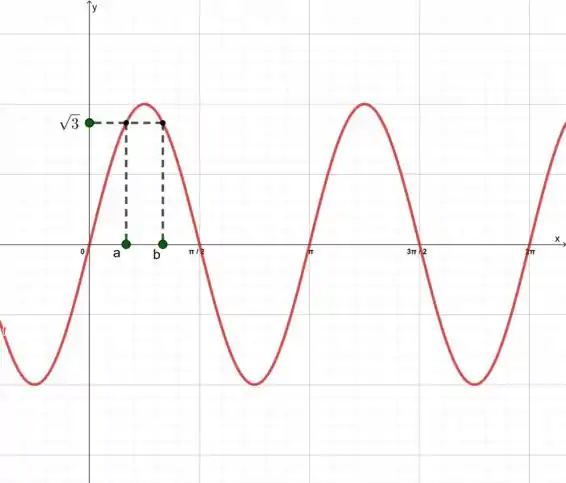
Qual o valor de a e b indicados no eixo x?
Passo 1
Acho que você concorda comigo que essa função não está nada amigável e receptiva, está bem complicado de chegarmos a alguma conclusão sobre ela.
Vamos tentar simplificar?
Fazendo esses produtos notáveis, temos
Beeeem mais bonitinha, né? =D
Passo 2
Beleza, agora precisamos ver os pontos do primeiro quadrante que terão o , como nos mostra o enunciado. Basta igualarmos a nossa função a . Fica assim ó:
Dividindo os dois lados por 2, temos:
Tá, mas no que isso adianta a gente?
A expressão que está ao lado esquerdo é igual ao seno de um arco duplo, portanto, teremos:
Agora, pensa comigo no seguinte, quais são os valores que tem como o seno o ?
O seno de 60° e o de 120° graus, por estarem no 1º e 2º quadrantes, são positivos.
Ou seja, teremos:
Concluimos então que
Resposta
e