UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 14, Questão 31
Um retângulo ABCD é inscrito em uma circunferência de raio . Denote por o ângulo entre o
lado e a diagonal .
- Mostre que a área do retângulo é .
- Mostre que dentre todos os retângulos inscritos na circunferência, a maior área possıvel é
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de pré-cálculo .Essa é bem tranquila, vamos fazer um desenho ilustrando a situação
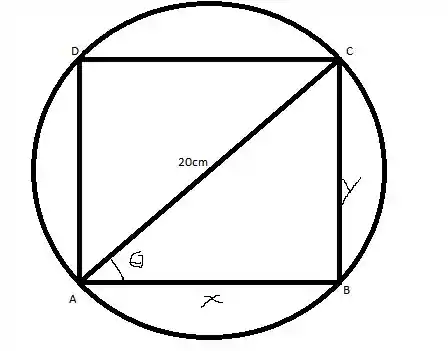
bem, vamos obter os valores de em função de . Então temos:
logo, a área do retângulo é:
Passo 2
Agora vamos para a letra , que pede para mostrar que dentre todos os retângulos inscritos na circunferência, a maior área possıvel é .
Na letra , vimos que a área é
Logo como , a maior área vai ocorrer quando e seu valor é
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima
Exercícios de Livros Relacionados
Faça o gráfico da função f ( x ) = s e n ( 1 x ) Qual o domínio e a imagem de f ? f é uma função periódica? Justifique sua resposta.
Esboce o gráfico.y = x sen (1)/(x)
Determine o domínio e esboce o gráfico.f (x) = cosec x
Mostre que para todo x , com cos (x)/(2) != 0 , tem-se:sen x = (2 tg (x)/(2))/(1 + tg^2 (x)/(2))
Nos exercícios 39-42, expresse a quantidade em termos de sen x e cos x .39. cos ( π + x )