19. Sejam , e os vértices de um triângulo retângulo com ângulo reto em e sejam e as medidas dos catetos e , respectivamente. Se é o ponto médio do cateto , então a tangente do ângulo é igual a
Passo 1
Oi, galerinha! Tudo bom? O problema nos descreve um triângulo retângulo e pede para calcularmos a tangente de um ângulo.
Pela descrição do enunciado, temos o seguinte triângulo,
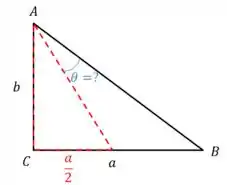
Ou seja, ele quer saber, quem é .
Passo 2
Vamos começar pela definição de tangente que é
Deste modo, a tangente do ângulo será,
Já a tangente do ângulo será
Mas o problema quer saber , que é o nosso ângulo , que é
Se queremos achar a tangente , podemos fazer
Agora vamos calcular isso aí!
Passo 3
Para quem não lembra, quando precisamos calcular a tangente de uma subtração de ângulos, nós temos essa fórmulinha aqui
Ou seja,
No passo anterior, vimos quanto valia e . Substituindo,
Ajeitando,
Prontinho!