Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Funções Trigonométricas – Parte 1

Ver Teoria
Exercício 1234567891011121314151617181920212223242526

Enunciado

Diga se as afirmações abaixo são verdadeiras ou falsas:

  1. O seno de um ângulo θ é calculado através da fórmula s e n θ = c a t e t o   a d j a c e n t e h i p o t e n u s a ;
  2. O cosseno de um ângulo θ é calculado através da fórmula c o s θ = c a t e t o   a d j a c e n t e h i p o t e n u s a ;
  3. As relações s e n θ , cos ⁡ θ ,   t g θ são definidas a partir de um triângulo retângulo.
  4. A tangente de um ângulo θ é calculada através da fórmula t g θ = c a t e t o   a d j a c e n t e   a   θ c a t e t o   o p o s t o   a   θ

Passo 1

Fala Aíí!! Vamos analisar cada uma das afirmações e verificar quais são verdadeiras e quais são falsas!

Na letra (a) temos a afirmação “O seno de um ângulo θ é calculado através da fórmula s e n θ = c a t e t o   a d j a c e n t e h i p o t e n u s a " .

Vamos relembrar o que é o seno de um ângulo?

O s e n o θ é a razão entre a medida do cateto oposto θ e a hipotenusa de um triângulo retângulo. Ou seja, é o resultado da divisão da medida do cateto oposto pela medida da hipostenusa

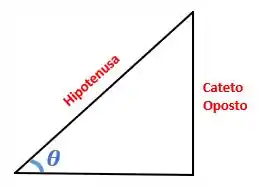
Pra lembrar a gente pode até brincar com as palavras. Olha para o ângulo e para o cateto oposto, você concorda que o cateto oposto está longe do ângulo? Então, podemos lembrar que ele está “sem” o ângulo, assim a relação dele com a hipotenusa é o “seno”.

Ou seja, o nosso s e n θ é

Assim, a afirmação da letra (a) é falsa!

Passo 2

b) Para verificar se a afirmação da letra (b) é verdadeira ou falsa vamos relembrar o que é o cosseno de um ângulo θ . O cosseno é a razão entre a medida do cateto adjacente a θ   e a hipotenusa do triângulo. Visualmente, teremos

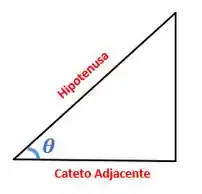
E aqui também tem aquele joguinho de palavras. Olha para o ângulo e para o cateto adjacente, você concorda que o cateto adjacente está “colado” no ângulo? Então a relação entre a hipotenusa e o cateto que está “colado” no ângulo é o “cosseno”.

Assim,

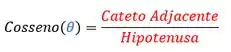
Ou seja, a afirmação é verdadeira!

Passo 3

c) A afirmação que devemos avaliar se é verdadeira ou falsa é “As relações s e n θ , cos ⁡ θ ,   t g θ são definidas a partir de um triângulo retângulo.” Essa afirmação é verdade, pois o s e n θ , cos ⁡ θ ,   t g θ relacionam as medidas dos lados de um triângulo retângulo com as medidas de seus ângulos.

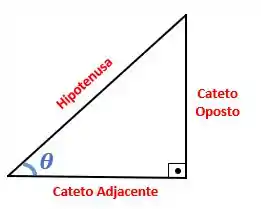
Lembrando que um triângulo é retângulo quando um de seus ângulos é igual a 90 ° .

Passo 4

d) A última afirmação se refere a tangente de um ângulo θ . A tangente é a única relação que não envolve a hipotenusa de um triângulo. Ela é dada por

Onde, no triângulo retângulo

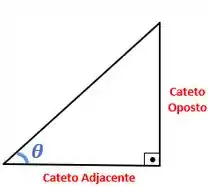
Ou seja, a afirmação da letra (d) é falsa!!

Resposta

  1. Falsa
  2. Verdadeira
  3. Verdadeira
  4. Falsa

Exercícios de Livros Relacionados

Faça o gráfico da função f ( x ) = s e n ( 1 x ) Qual o domínio e a imagem de f ? f é uma função periódica? Justifique sua resposta.
Esboce o gráfico.y = x sen (1)/(x)
Determine o domínio e esboce o gráfico.f (x) = cosec x
Mostre que para todo x , com cos (x)/(2) != 0 , tem-se:sen x = (2 tg (x)/(2))/(1 + tg^2 (x)/(2))
Nos exercícios 39-42, expresse a quantidade em termos de sen ⁡ x e cos ⁡ x .39. cos ⁡ ( π + x )