Determine o domínio e a imagem da função e esboce seu gráfico.
Passo 1
Vamos lááá! Primeiro vamos determinar o domínio da função
Sabemos que o domínio da função é o conjunto dos números reais, certo?!
Assim, se você reparar, na função do nosso enunciado, estamos apenas somando , o que não interfere no domínio. Assim, ele continuará sendo o conjunto dos números reais. Portanto,
Beleza?!

Passo 2
Agora vamos determinar a Imagem da função .
Como podemos fazer isso??
Vamos substituir os valores máximo e mínimo de e assim a imagm será o intervalo entra esses dois valores, beleza?!
Bom, a função varia entre e
Assim,
Aplicando esses valores na função , temos
Para :
Da mesma forma, para :
Portanto, a Imagem de é:
Show de bola?!

Passo 3
Para esboçarmos o gráfico da função, basta esboçarmos o gráfico de e somarmos 2 a cada ponto. Ou seja,vamos transladar o gráfico para cima 2 casas:
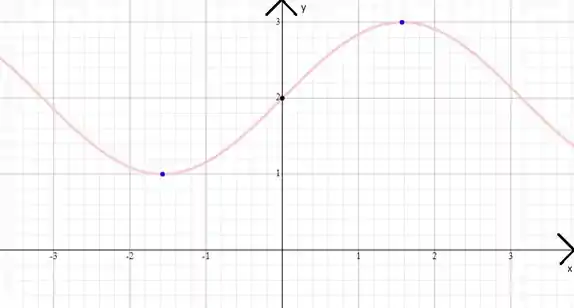
Show de bola?!
Resposta
Ei, a resposta está no passo a passo :)