20. Sejam e números reais positivos. Na figura abaixo, a linha pontilhada representa o gráfico da função e a linha contínua representa o gráfico da função .
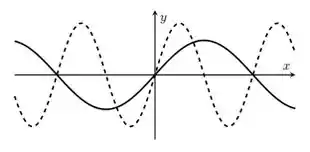
Pode-se afirmar que
- e
- e
- e
- e
- e
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos o gráfico de duas funções, onde nelas temos duas constantes e , e baseado no gráfico temos que estimar quanto vale cada constante.
Para fazer isso, vamos olhar as coincidenias entre as funções: ambas são uma função seno. Para quem não lembra a função seno tem essa cara:
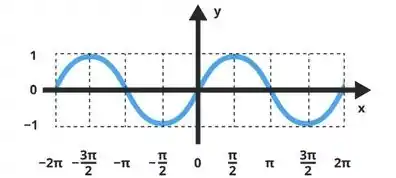
Repara que ela atinge valores máximos e mínimos em , onde é um número inteiro impar. Variando entre e . Além disso, a função é igual a zero em e , onde é qualquer número inteiro.
Então vamos olhar para esses pontos de máximo e mínimo para estimar os valores de e .
Bora lá!
Passo 2
Vamos começar descobrindo qual intervalo que está contido. Para isso, vamos olhar para a função , que está pontilhada no gráfico. Repara que o máximo dela será . Uma vez que a função seno tem valor máximo em e a nossa tem um multiplicando a função seno. Ou seja,
Agora vamos comparar o máximo da nossa com o máximo da nossa . Repara que o máximo da nossa em vermelho, é menor que o da nossa , em azul.
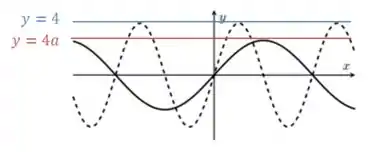
Ou seja, quando o seno,
Temos que
E como no ponto máximo
Logo é uma valor fracionario,
Agora vamos descobrir quem é !
Passo 3
Repara que o máximos de e não coincidem em !
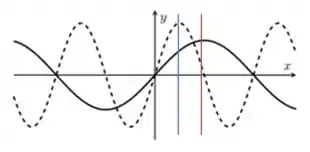
Ou seja, não é um número inteiro, logo
Prontinho!