A imagem da curva , está melhor representada em
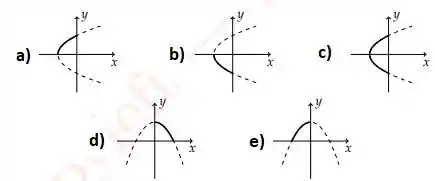
Passo 1
Fala galerinha, prontos para mais uma questão de identificação de curvas?
A curva fornecida nesse problema é
Como , temos que
Da segunda equação, tiramos:
Substituindo na primeira:
Assim,
Logo,
Passo 2
Essa parábola está bem representada nas alternativas A, B e C. Temos que identificar apenas qual a parte da parábola que corresponde à curva!
Note que
Assim,
Portanto,
Logo,
Com isso, apenas a parte da parábola no segundo quadrante deve ser considerada. A resposta está na alternativa A 😊
Resposta
Alternativa A.