Banco de Questões - Estácio de Cálculo Diferencial e Integral II da UNESA - AV3
Cálculo Diferencial e Integral II - UNESA
Sejam funções uniformes e contínuas em um domínio conexo limitado por uma curva fechada . Então, pelo Teorema de Green:
Calcule a integral de linha:
Sobre a circunferência unitária , ; utilizando o Teorema de Green.
Ver solução completaEncontre o vetor aceleração de uma partícula para o instante , onde sua posição é dada pelo vetor
Seja . Calcular o valor da integral tripla da função em relação às variáveis e onde varia no intervalo , varia no intervalo e varia no intervalo .
Se resistores elétricos de , , ohms são conectados em paralelo para formar um resistor de ohms, o valor de pode ser encontrado a partir da equação:
Encontre o valor de quando , e ohms.
Ver solução completaUm competidor em sua asa-delta realiza uma espiral no ar cujo vetor posição é . Esta trajetória faz lembrar a de uma hélice. Para o intevalo de tempo , encontre o módulo da velocidade da asa-delta no instante .
Ver solução completaCalcule a aceleração de um partícula com vetor de posição em indicando a única resposta correta.
Calcule a aceleração de um partícula com vetor de posição . Indique a única resposta correta.
Seja . Calcular a integral da função sobre a curva definida por , onde varia no intervalo .
Ver solução completaA equação de Laplace tridimensional é:
As funções que satisfazem à equação de Laplace são ditas funções harmônicas.
Considere as funções:
Identifique as funções harmônicas:
Integre sobre o segmento de reta que une a origem ao ponto passando primeiro por . Dado a parametrização , .
Ver solução completaSeja . Calcular o valor da integral tripla da função em relação às variáveis , e onde varia no intervalo , varia no intervalo e varia no intervalo .
Determine a derivada direcional da em , sendo um versos dado pelo ângulo .
Então a derivada direcional da no ponto será:
Quando uma curva , passa pelo domínio de uma função no espaço, os valores de ao longo da curva são dados pela função composta . Quando integramos essa função composta em relação ao comprimento de arco de a , calcula-se a integral de linha de ao londo da curva.
Portanto .
Calcule a integral de linha onde é a hélice circular dada por , .
Aplique o Teorema de Green para calcular a integral:
Onde a curva é o triângulo limitado por , e .
Marque dentre as opções a que representa uma equação cartesiana para a equação polar .
Seja . Calcular a integral da função sobre a curva definida por onde varia no intervalo .
Ver solução completaSeja . Calcular o valor da integral tripla da função em relação às variáveis , e onde varia no intervalo , varia no intervalo e varia no intervalo .
Considere a função . Calcular o gradiente da função
(a) +
(b) +
(c) +
(d) +
(e) +
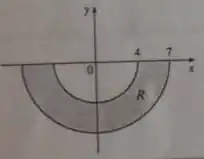
Ver solução completaCalcule a área e faça um esboço do gráfico da região representada pela integral:
Ver solução completa