Sejam funções uniformes e contínuas em um domínio conexo limitado por uma curva fechada . Então, pelo Teorema de Green:
Calcule a integral de linha:
Sobre a circunferência unitária , ; utilizando o Teorema de Green.
Passo 1
O segredo aqui é não pensar demais: vamos dar uma olhada na integral que queremos resolver:
Ou seja:
A fórmula que o enunciado deu diz que, pelo Teorema de Green, podemos igualar aquele integral de linha à seguinte integral de superfície:
Beleza, já aplicamos o teorema de Green, agora a questão é: como resolver essa integral de superfície?
Passo 2
O primeiro passo é resolver as derivadas parciais que estão dentro da integral:
Agora vamos substituir isso na integral:
Opa, já ficou tudo bem fácil, a gente sabe que isso aqui:
É simplesmente a área da região ! Ou seja, a resposta do nosso problema é simplesmetne vezes a área da região .
Passo 3
Bom, é a região delimitada pela curva , mas quem é a curva ? O enunciado já disse: é uma circunferência unitária!
Qual é a área de uma circunferência unitária? (ou seja, uma circunferência de raio )
Mas cuidado! Na parametrização que o enunciado deu, o ângulo só ia de até , ou seja, temos algo assim:
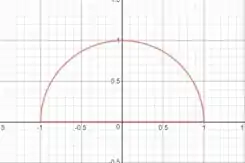
Então vamos pegar só metade da área do círculo unitário!
E como a nossa resposta é quatro vezes a área da região:
Pronto!
Resposta
A integral vale .