Aplique o Teorema de Green para calcular a integral:
Onde a curva é o triângulo limitado por , e .
Passo 1
Vamos começar desenhando a curva no plano cartesiano. O nosso triângulo é definido por três retas:
As duas primeiras retas são mais fáceis de desenhar.
Se você tiver dificuldade para desenhar a terceira reta, escolhe dois pontos quaisquer para calcular e depois só desenhe a reta que passa por eles:
Então nosso triângulo é esse aqui:
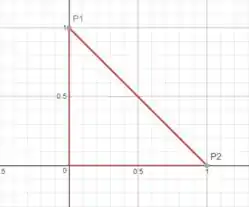
E a região é toda a área desse triângulo.
Passo 2
Agora vamos lembrar o que diz o teorema de Green:
No nosso caso:
E vamos calcular as derivadas parciais:
Substituindo isso na fórmula do teorema:
Passo 3
Agora precisamos calcular essa integral:
Lembrando que é essa região em verde:
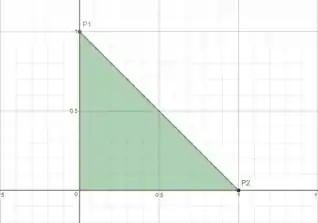
Como podemos integrar a função nessa região? Primeiro temos que escolher uma variável que vai ser limitada por constantes, vamos tomar a , por exemplo, entre quais números ela varia?
Ok, agora pegue um qualquer nesse intervalo. Com esse fixo, em que intervalo o varia?
Nós vamos do até o valor da função naquele , ou seja:
Ótimo, agora vamos jogar isso na integral:
Passo 4
Agora está tudo pronto para resolvermos:
Começamos integrando em relação a , lembrando que:
Então:
Agora vamos arrumar um pouco esse polinômio:
E substituindo isso na integral dupla:
Agora é só integrar esse polinômio em relação a , sabendo que:
Então:
E esse é o valor da nossa integral!
Resposta
Letra (a).