Calcule a área e faça um esboço do gráfico da região representada pela integral:
Passo 1
Aqui não tem segredo. A primeira informação que podemos tirar da nossa integral é que todos os pontos no interior da região tem coordenada dentro desse intervalo aqui:
Então vamos representar isso no plano. Por enquanto só sabemos que estamos em algum lugar nessa região vermelha:
Passo 2
A segunda informação que essa integral dá é que para cada ponto nessa região, o varia entre duas funções:
Essa você sabe desenhar, é uma reta decrescente (já que o coeficiente angular é negativo) com inclinação e que cruza o eixo no ponto . No seu desenho não precisa ser nada perfeito, é só um esboço:

E a outra função é simplesmente uma parábola:
O sinal negativo nos diz que a parábola é “aberta” para baixo, e o nos diz que ela toca o eixo no ponto . Com isso nós definimos nossa região:
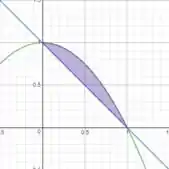
Passo 3
Agora, para calcular a área, podemos simplesmente resolver a integral:
Primeiro integramos em relação a :
Agora integrando em relação a , a integral indefinida é , ou seja:
Resposta
A área da região é .