Integre sobre o segmento de reta que une a origem ao ponto passando primeiro por . Dado a parametrização , .
Passo 1
A ideia é a seguinte: vamos integrar aquea função sobre o seguinte caminho: saímos da origem e vamos para o ponto , e dali seguimos para .
Os pontos e não são colineares, então apesar de que a questão ter mencionado “um segmento de reta que passa pelos três pontos”, é impossível existir um segmento como esse. Por isso, não poderemos usar a parametrização que o enunciado deu.
Mas ainda podemos resolver a questão!
Precisamos, na verdade, fazer um caminho como esse para passar pelos três pontos:
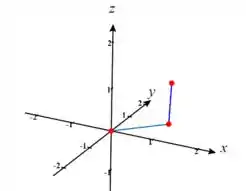
Passo 2
Vamos começar pela primeira parte: de para . O primeiro passo é achar uma parametrização simples para esse trajeto.
Se tomarmos essa parametrização:
E fizermos o variar de até , teremos percorrido exatamente o caminho certo.
Passo 3
Agora lembre da fórmula para montar uma integral de linha (já substituímos nossos limites de integração):
Já podemos calcular . Primeiro derivamos:
E depois achamos o módulo desse vetor:
Além disso, podemos achar :
E substituindo , , :
Passo 4
Agora podemos substituir tudo na integral:
Agora a integral é bastante simples:
Passo 5
Agora precisamos ir do ponto até . Perceba que nesse caso e se mantém constantes e iguais a , e só o muda. Nossa parametrização pode ser a seguinte:
E vamos fazer variar entre e .
Lembrando da fórmula de antes:
Começamos calculando . A derivada é:
E o módulo desse vetor é:
Por último, precisamos obter . Para isso, é só substituir , e :
Passo 6
Agora é só jogar tudo isso naquele fórmula de antes:
E a integral fica bastante simples:
Somando os dois valores que encontramos:
Resposta
O valor da integral no caminho escolhido é .