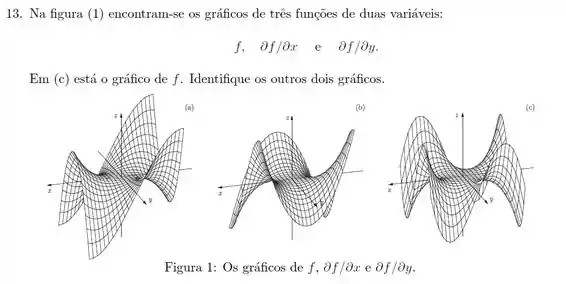
Passo 1
É o seguinte: temos que descobrir, com base no gráfico da função , qual é o gráfico da derivada parcial de em relação a e em relação a .
Vamos primeiro observar bem o gráfico de :
Temos que nossa função, em alguns momentos meio que tem um comportamento constante no eixo e em outros momentos, tem um comportamento constante ao longo do eixo .
Passo 2
Beleza, agora, o que é a derivada parcial em relação a ?
É quando fixamos os valores de da nossa função como constante e derivamos em relação a , observando quando o comportamento da nossa função com relação a variável .
O mesmo é válido para a derivada parcial em relação a , só que trocando o por no que eu acabei de dizer: fixamos os valores de da nossa função como constante e derivamos em relação a , observando quando o comportamento da nossa função com relação a variável .
Passo 3
Agora, observando bem as figuras e .
Conseguimos ver que na figura :
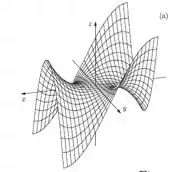
Temos que o comportamento dessa função ao longo do eixo é idêntico ao comportamento da nossa função da figura ao longo do eixo .
Isso significa que para essa figura, fixamos os valores de da nossa função como constante e derivamos em relação a . Logo, ela representa a .
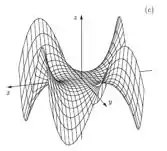
Já se observarmos a figura :
Temos que o comportamento dessa função ao longo do eixo é idêntico ao comportamento da nossa função da figura ao longo do eixo .
Assim, para essa figura, fixamos os valores de da nossa função como constante e derivamos em relação a . Logo, ela representa a .
Resposta
![]()