UFF, Cálculo IIB, Listas GMA, Lista 3, exercício 11.
Seja
Calcule e e interprete geometricamente.
Passo 1
Bem, primeiramente, vamos encontrar as derivadas parciais dessa função. Daqui a pouco a gente interpreta isso geometricamente, ok?
Vamos lá. Começando por .
Substituindo no ponto
Passo 2
Agora vamos para
Substituindo no ponto :
Passo 3
Agora vamos a interpretação geométrica:
Quando derivamos a função em relação a , mantemos a variável fixa. Com isso, temos uma função de uma variável ), cujo gráfico é a curva de interseção entre o gráfico da função e o plano .
Essa curva tem uma reta tangente no ponto , que pertence a esse plano .
A derivada parcial representa, então, a inclinação dessa reta tangente em relação ao eixo .
Dá uma olhada:
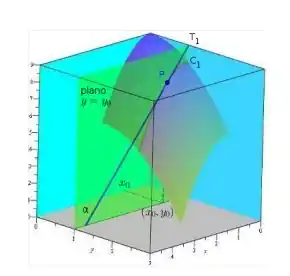
Assim, a derivada parcial representa o ângulo de inclinação em relação ao eixo da reta tangente ao gráfico de no ponto , pertencente ao plano .
Além disso, como é menor que zero, esse ângulo de inclinação em relação ao eixo é maior que que 90°. (Nessa imagem , portanto, a inclinação é menor que 90°).
O mesmo vale para a derivada parcial em relação a . Assim, representa o ângulo de inclinação em relação ao eixo da reta tangente ao gráfico de no ponto , pertencente ao plano . E, como é menor que zero, esse ângulo de inclinação em relação ao eixo y é maior que que 90°