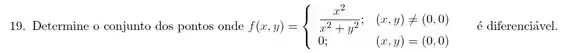
Passo 1
Como nossa função tem duas definições, uma para e outra para , vamos analisar a diferenciabilidade dela separadamente.
Para a função é diferenciável pois é o quociente entre duas funções polinomiais, que são diferenciáveis.
Passo 2
Já para , precisamos testar a continuidade da função. Vamos lá.
Para essa função ser contínua na origem, basta que o limite dela, na origem, seja o próprio valor que ela assume no ponto , ou seja,
Mas, aqui vem um truque: é muito mais fácil provar que o limite não existe!
E como que eu sei disso? Porque o grau do numerador é igual ao grau do denominador.
Então vamos tentar.
Passo 3
Podemos calcular o valor do limite pra uma infinadade de caminhos, então vamos escolher os mais fáceis! Uma boa é testar primeiro e . Então vamos lá:
Passo 4
Agora testando :
Opa! Obtivemos 2 resultados diferentes! Portanto o limite não existe, e a função não é contínua na origem.
Passo 5
E sabemos que
Logo, é diferenciável em todo o , menos na origem.
Resposta
![]()