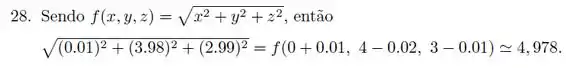Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Aproximação Linear de uma Função de Várias Variáveis

Ver Teoria
Exercício 3212345678910111213141516171819202122232425262728293031333435363738394041

Enunciado

Passo 1

A expressão da aproximação linear pra uma função de três variáveis é dada por:

L x , y , z = f x 0 , y 0 , z 0 + f x x - x 0 + f y y - y 0 + f z z - z 0

Para isso, precisamos das derivadas parciais e do valor da função num ponto que seja o mais próximo possível do ponto de interesse.

Vamos usar o ponto

P 0 = 0,4 , 3

Porque ele é próximo do ponto em que x = 0,01 , y = 3,98 e z = 2,99 .

Agora, a gente ainda precisa definir a função apropriada, pra poder continuar a questão:

f x , y , z = x 2 + y 2 + z 2

Passo 2

Agora achamos as derivadas parciais de f .

F x , y , z = x 2 + y 2 + z 2

∂ f ∂ x = 1 2 x 2 + y 2 + z 2 ∙ 2 x = x x 2 + y 2 + z 2

∂ f ∂ y = 1 2 x 2 + y 2 + z 2 ∙ 2 y = y x 2 + y 2 + z 2

∂ f ∂ z = 1 2 x 2 + y 2 + z 2 ∙ 2 z = z x 2 + y 2 + z 2

Passo 3

Substituindo em P 0 = 0,4 , 3 ,

∂ f ∂ x = 0 0 2 + 4 2 + 3 2 = 0

∂ f ∂ y = 4 0 2 + 4 2 + 3 2 = 4 5

∂ f ∂ z = 3 0 2 + 4 2 + 3 2 = 3 5

Tranquilo?

Passo 4

A aproximação linear fica então

L x , y , z = f 0,4 , 3 + f x x - 0 + f y y - 4 + f z z - 3

L x , y , z = 0 2 + 4 2 + 3 2 + 0 x - 0 + 4 5 y - 4 + 3 5 z - 3

L x , y , z = 5 + 4 5 y - 16 5 + 3 5 z - 9 5

L x , y , z = 4 5 y + 3 5 z

Passo 5

Agora, pra descobrir o valor aproximado que a questão pede é só substituir x = 0,01 , y = 3,98 e z = 2,99 nessa expressão que acabamos de achar, porque

f ( x , y , z ) ≈ L ( x , y , z )

Então

f 0,01 ; 3,98 ; 2,99 ≈ 4 5 ∙ 3,98 + 3 5 ∙ 2,99

f 0,01 ; 3,98 ; 2,99 ≈ 4,978

Resposta

Exercícios de Livros Relacionados

O índice de sensação térmica W é a temperatura que se sente quando a temperatura real for T e a velocidade do vento, v ; portanto, podemos escrever W = f T , v . A tabela de valores a seguir foi extra
A altura h de ondas em mar aberto depende da velocidade do vento v e do tempo t durante o qual o vento se manteve naquela intensidade. Os valores da função h = f( v , t ) são apresentados na seguinte
Explique por que a função é diferenciável no ponto dado. A seguir, encontre a linearização L ( x ,y ) da função naquele ponto. f x ,y = 1 + y 1 + x ( 1 ,3 )
Utilize a tabela do Exemplo 3 para encontrar a aproximação linear da função humidex quando a temperatura está próxima de 94 °F e a umidade relativa do ar é de aproximadamente 80 % . Estime também o hu
Verifique a aproximação linear em 0,0 . 2 x + 3 4 y + 1 ≈ 3 + 2 x - 12 y