Um balão se desloca horizontalmente no ar com rapidez constante. Em dado instante uma pedra cai do balão, permanece no ar durante e atinge o solo segundo uma direção que faz um ângulo de com a vertical, como na figura abaixo. Desprezando-se a resistência do ar, responda:
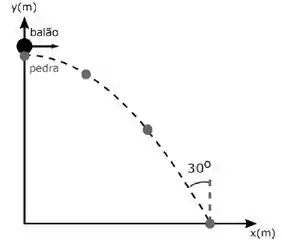
Qual é a rapidez do balão?
(A)
(B)
(C)
(D)
(E)
Passo 1
Quando a pedra é solta, ela apresenta a mesma velocidade do balão na horizontal.
Nesse “lançamento horizontal”, a pedra vai ganhando velocidade apenas na direção vertical enquanto a componente horizontal permanece a mesma.
Então, quando ela chega ao chão a componente horizontal da sua velocidade ainda é a mesma que a do balão:
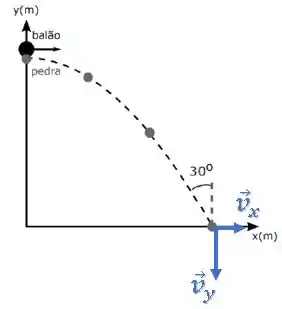
Portanto, basta descobrirmos a componente que matamos o problema.
Passo 2
Podemos relacionar a componente e a partir do ângulo de 30° do vetor velocidade da pedra:
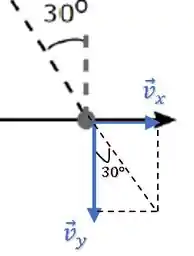
Então, vamos encontrar a componente da velocidade da pedra no momento que ela bate no chão.
Passo 3
A componente vertical funciona assim como no lançamento vertical, nesse caso uma queda livre.
Portanto, podemos utilizar a equação de um movimento retilíneo uniformemente acelerado:
A velocidade inicial (na vertical) é zero e a aceleração é a gravidade:
Sabemos que o tempo de vôo foi de :
Passo 4
Podemos “trasportar” o vetor para o cateto oposto ao ângulo de 30°:
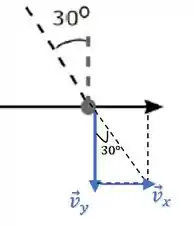
Substituindo os valores, temos:
Essa será a velocidade do balão.
Ficamos com a alternativa (A).
Resposta
Letra (A)