USP – Física I (Química) – P1 – Questão 4
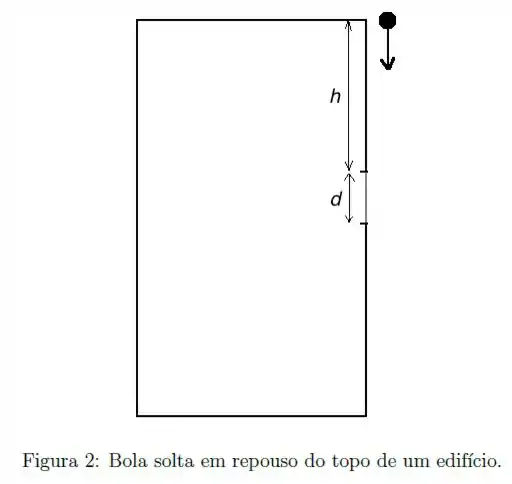
Uma bola é solta do topo de um edifício com velocidade inicial zero (veja a Figura ). A bola leva para passar por uma janela de comprimento que está a uma distância do topo.
- Qual era a velocidade da bola quando ela passou pelo topo da janela?
- Qual a distância ?
Passo 1
Oi, tudo bem? Esse problema tem jeito de ser cabuloso, mas vou te ajudar! Temos uma bolinha que é solta a partir do repouso do alto de um prédio: MOVIMENTO QUE QUEDA LIVRE!
Sendo assim, antes de mais nada, vamos relembrar das equações que regem esse movimento
A ideia para resolver o que é pedido é partir dos dados fornecidos, encontrar a equação que mais se adequa! Sempre pensando no que temos (posição, velocidade etc) com o que queremos! Esse é o segredo!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Letra (a) Nesse primeiro item o problema pede para calcularmos a velocidade da bolinha no topo da janela
Ele nos diz que o tempo para passar do alto da janela até o ponto mais baixo é de , e que a distância percorrida nesse intervalo de tempo é de
Então supondo que a posição inicial seja o topo e a posição ao final dos seja embaixo da janela
Beleza? Então buscamos uma equação que tenha: tempo, posição final e inicial e o tempo!
Podemos usar a primeira!
Lembrando que , podemos achar :
Substituindo os valores temos
Show!
Bora para a letra (b)?
Passo 3
Letra (b): agora o problema pergunta a altura !
Acabamos de determinar a velocidade no topo da janela, não é mesmo? E se você olhar com pouco de atenção para o desenho do movimento, verá que o topo da janela é o “final” do movimento que parte do topo do prédio até o início da janela!
Sendo assim, a velocidade que calculamos passa a ser nossa “velocidade final”. A velocidade inicial é zero, pois a bolinha parte do repouso. A posição inicial é a altura total do prédio , e a posição final é a diferença entre a altura do prédio e a distância . Assim a distância percorrida é
Reunindo os dados:
E comparando com as fórmulas
Vemos que vamos usar a do meio!
Substituindo os valores
Ufa! Terminamos!
Bora pra próxima?