Dois projéteis 1 e 2 de mesma massa são lançados simultaneamente e horizontalmente de alturas e (diferentes) em relação ao solo. Verifica-se que ambos atingem o mesmo ponto A no solo, conforme a figura:
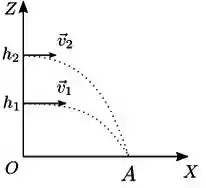
Qual a única das grandezas a seguir que é a mesma para os dois projéteis?
(a) Vetor aceleração média entre o instante de lançamento e o imediatamente anterior ao projétil atingir o solo.
(b) Vetor velocidade média entre o instante de lançamento e o imediatamente anterior ao projétil atingir o solo.
(c) Direção do vetor velocidade instantânea no instante imediatamente anterior ao projétil atingir o solo.
(d) Intervalo de tempo entre o instante de lançamento e o imediatamente anterior ao projétil atingir o solo.
Passo 1
Temos duas partículas sendo lançadas horizontalmente a partir de alturas diferentes, porém elas atingem o chão no mesmo ponto (mesmo alcance).
O que podemos descobrir sobre as velocidades?
O tempo de queda depende apenas da altura, podemos calcular esse tempo com aquela expressão:
Isso acontece porque a aceleração da gravidade é constante:
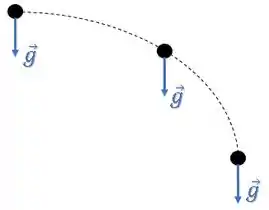
Assim, analisando apenas o movimento vertical da partícula, temos um movimento uniformemente acelerado (MUV) com velocidade inicial zero :
Tá... okay. E daí?
Como a altura da partícula 2 é maior que a altura da partícula 1 , o tempo de queda em 2 também será maior que em 1:
Até aí beleza, e as velocidades?
Velocidade horizontal:
Como a partícula 2 demora um tempo maior para percorrer uma mesma distância , ela está mais “devagar” horizontalmente que a partícula 1.
Então, a velocidade horizontal 2 é menor que a da partícula 1:
Isso acontece para todos os instantes do trajeto, já que a velocidade horizontal é constante nos lançamentos.
Velocidade vertical:
Já vimos que, Inicialmente, ambas são nulas:
Mas e no momento em que as partículas atingem o chão?
A partícula mais alta vai chegar no chão com uma velocidade maior, certo?
Isso mesmo! A partícula 2 “sofreu” a aceleração da gravidade por mais tempo e por isso sua velocidade vertical vai ser maior que a da partícula 1:
Okay, agora vamos pegar as alternativas.
Passo 2
(a) Vetor aceleração média entre o instante de lançamento e o imediatamente anterior ao projétil atingir o solo.
Bom, a única aceleração que as partículas sofrem é a aceleração da gravidade , que é constante em todos os instantes do movimento:
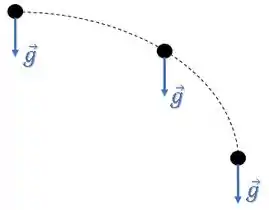
Então, o vetor aceleração média nos dois casos é igual ao vetor da aceleração da gravidade:
Assim, as duas partículas têm o mesmo vetor aceleração média.
A alternativa (a) está correta e achamos nossa resposta.
Mas vamos dar uma olhada nas outras também.
Passo 3
(b) Vetor velocidade média entre o instante de lançamento e o imediatamente anterior ao projétil atingir o solo.
O vetor velocidade média é dado pelo vetor deslocamento sobre o intervalo de tempo :
Então, o vetor velocidade média estará na mesma direção do vetor deslocamento.
Os vetores deslocamentos são:
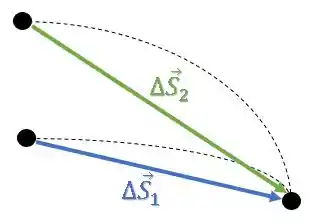
Como eles estão em direções diferentes, os vetores velocidade média também estarão em direções diferentes, logo:
A alternativa (b) está incorreta.
Passo 4
(c) Direção do vetor velocidade instantânea no instante imediatamente anterior ao projétil atingir o solo.
Vimos lá no Passo 1, que as componentes das velocidades verticais no instante final são diferentes, sendo a da partícula 2 maior:
Enquanto as componentes horizontais não mudam ao longo do movimento e também são diferentes entre si. Porém dessa vez, a da partícula 1 é maior:
Será que essas componentes acabam se compensando e no final resultam em vetores velocidade instantânea iguais?
Na verdade, isso não acontece.
As velocidades são sempre tangentes à trajetória:
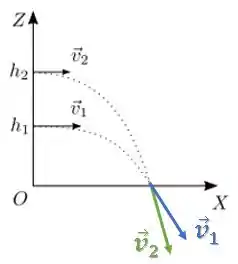
O movimento de lançamento horizontal tem uma trajetória de uma parábola.
Como o vértice dessas parábolas (ponto inicial) estão em alturas diferentes, mas partem do mesmo “x”, não tem como essas parábolas se encontrarem e ainda serem tangentes em um ponto. (argumentozinho de cálculo chato né... hahah)
É mais fácil pensar em um contra-exemplo do que justificar o “nunca”, e podem ser quaisquer valores, desde que diferentes.
Se a gente ir alterando um desses , o vetor velocidade instantânea naquele ponto do solo vai mudando de direção, né?
Então, os vetores velocidade instantânea e vão ser diferentes entre si e a afirmativa está errada.
A alternativa (c) está incorreta.
Passo 5
(d) Intervalo de tempo entre o instante de lançamento e o imediatamente anterior ao projétil atingir o solo.
Já vimos no Passo 1, que os tempos de queda dependem da altura.
Assim, como as alturas e são diferentes, temos tempos de queda diferentes:
A alternativa (d) está incorreta.
Resposta
Letra (a)