Um menino gira uma pedra em um círculo horizontal de raio 1,5 m a uma altura de 2,0 m acima do chão. A corda quebra e a pedra voa horizontalmente até bater com o chão após percorrer uma distância de 10 m. Qual é a magnitude da aceleração centrípeta da pedra durante o movimento circular?
Passo 1
Oi pessoal, tudo bem? O problema nos disse que temos uma pedra girando (em um plano horizontal) até que essa corda quebra e a pedra sai voando horizontalmente a partir da altura que essa pedra estava girando .
Na figura da esquerda está esquematizado o movimento da pedra quando gira em um plano horizontal (visto de cima) e na figura da direita está representado o instante em que a corda quebra e a pedra sai voando:
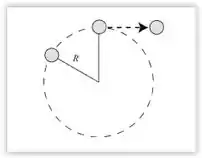
Reparem que pedra está descrevendo inicialmente um movimento circular uniforme, mas passa a descrever uma trajetória parabólica (lançamento horizontal) depois que a corda arrebenta.
Queremos descobrir a aceleração centrípeta , então precisamos do raio da trajetória e da velocidade linear (ou velocidade inicial do movimento parabólico).

Sendo assim, vamos usar as equações do MRUV (na direção vertical) e MRU (na direção horizontal) para calcular a velocidade, já que o raio foi dado!
Até aqui tranquilo? Mas calma, vou fazer com você passo a passo!
Passo 2
É sempre importante nesse tipo de exercício (lançamento de projétil) definir a direção/sentido que cada eixo representa. Aqui vamos escolher o sentido do semieixo positivo como sendo para cima e a origem.

No ponto em que a pedra deixa de descrever o movimento circular, as coordenadas da pedra durante o movimento parabólico são dadas por:
Nós sabemos que a pedra chega ao solo no ponto .
Isolando na equação da componente do deslocamento, obtemos que:
Agora bora substituir esse valor na primeira equação:
Tranquilo?
Passo 3
Agora com a velocidade inicial e o raio da trajetória circular, podemos calcular a aceleração!
Assim, o módulo da aceleração centrípeta será:
Tal que:
E é isso!
Espero ter ajudado!