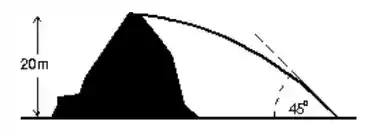
3. Uma bola é arremessada horizontalmente do topo de uma colina de de altura. A bola atinge o chão fazendo um ângulo de com a horizontal. Com que velocidade a bola foi lançada?
Passo 1
Olá, pessoal! Tudo bom? Aqui temos um probleminha de lançamento obliquo, onde o problema nos forneceu a altura e o ângulo de contato com o chão.
Como ele diz que a bola foi arremessada horizontalmente, temos que nossa velocidade no eixo é igual a zero.
E a velocidade no eixo é justamente o que ele nos pede. E podemos calcular por:
Onde é a posição final do objeto, é o que queremos descobrir, é o ângulo que faz com o solo e é o tempo até que o objeto atinja o solo.
Repara que não temos o tempo, então vamos ter que usar as informações da queda em relação ao eixo para achar o tempo e dai já vamos ter as informações para calcular a nossa velocidade.
Repara que se tra
Passo 2
Para calcularmos a queda em relação ao eixo vamos aplicar,
Como a altura é . Substituindo os valores, temos que
Resolvendo,
Agora que sabemos o tempo que o objeto chegou no chão, vamos achar a sua velocidade horizontal inicial.
Passo 3
Agora vamos aplicar,
Mas repara, que também não temos a distancia onde ele cai. Porém, podemos traçar uma reta com os referencias do desenho, formar um triangulo de pitagoras e calcular o nosso .
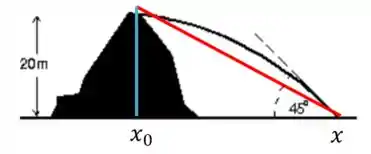
Temos, então, pela formula da tangente que será
Substituindo na formula,
Letra B!
Resposta
Letra B