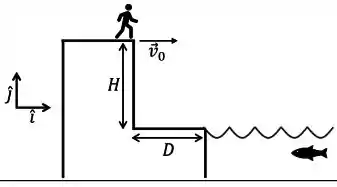
O brasileiro, radicado na Suíça, Laso Schaller detém o recorde mundial de salto livre em uma cachoeira. Na tentativa que levou ao recorde mundial Laso saltou uma cachoeira com cerca de de altura. Considere que para uma nova tentativa, Laso irá mergulhar de um penhasco com uma plataforma de salto horizontal, com velocidade horizontal () como mostra a figura abaixo.
Suas respostas devem ser dadas em função dos dados do problema: , , .
a) Qual deve ser o módulo mínimo de sua velocidade imediatamente após saltar do topo do penhasco para que não se choque com um degrau no pé do rochedo, com largura D e altura H abaixo do topo do penhasco?
b) Quanto tempo Laso irá levar para atingir a superfície da água?
c) Qual o vetor velocidade () de Laso no instante em que ele toca a superfície da água? Considere a velocidade inicial de Laso aquela encontrada no item a). Sua resposta deve estar em termos dos vetores unitários mostrados na figura.
Passo 1
Como o Laso salta do penhasco com uma velocidade na horizontal , ele vai realizar um Lançamento Horizontal.
Para analisar esse tipo de movimento, a gente trabalha separadamente com o movimento ao longo da direção (horizontal) e (vertical). Isso porque a única força atuando é a força peso na vertical...
Assim, o movimento ao longo da vertical será um Movimento Uniformemente Variado (aceleração constante), enquanto o movimento na horizontal será um Movimento Uniforme (velocidade constante).
Passo 2
Na letra (a), queremos a velocidade mínima para que ele alcance a água.
Para o Laso alcançar a água, ele tem que fazer no mínimo uma trajetória assim:
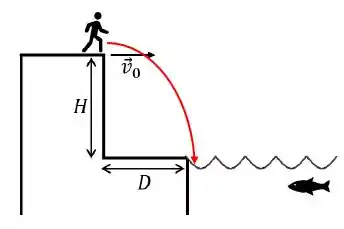
Ou seja, ele precisa percorrer na horizontal uma distância igual a , enquanto na vertical ele desce uma distância igual a .
Passo 3
Como ele já definiu que a direção positiva no eixo vertical é para cima, é conveniente colocar a origem nesse ponto aqui:
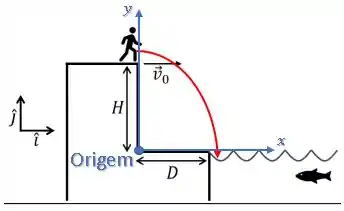
Agora, vamos escrever a equação da posição para cada um dos eixos.
Passo 4
No eixo , temos que sua velocidade vai se manter a mesma ao longo de todo o movimento (MU), então podemos usar:
Como sua posição inicial em é zero, temos:
No eixo , temos que o Laso sofre uma aceleração constante (MUV), então podemos usar:
Agora muito cuidado com o sentido da aceleração!
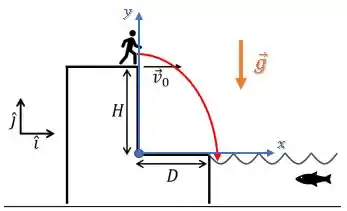
Como a aceleração da gravidade aponta para baixo, ela entra como negativa. Além disso, sua velocidade inicial em é nula, enquanto sua posição inicial é :
Passo 5
Agora, a ideia é que o tempo de queda é o mesmo tempo para percorrer uma distância na horizontal. Então, se chamarmos o tempo de , temos que na horizontal:
Podemos tirar outra relação com o movimento na vertical:
Como ele termina o movimento na altura zero, :
Substituindo esse valor na primeira relação, temos:
Podemos inverter o denominador e “entrar” com o na raiz elevado ao quadrado:
Esse é o valor mínimo de velocidade necessária para que o Laso chegue na água.
Passo 6
Na letra (b), queremos o tempo que leva para o Laso atingir a água, ou seja, o próprio .
Já achamos uma expressão para ele no item anterior, né?
Protinho, como e são dados do enunciado, já temos nossa resposta.
Passo 7
Na letra (c), queremos o vetor velocidade quando ele chega na água.
Bom, estamos analisando os movimentos separadamente (vertical e horizontal). O vetor velocidade vai ser a combinação das velocidades dos dois eixos:
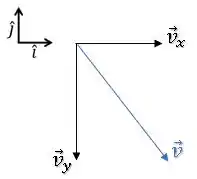
será a soma vetorial desses dois caras aí:
Passo 8
Mas quem são os vetores e ?
O módulo de nós já temos...
Como a velocidade na horizontal é a mesma durante todo o movimento, será igual à velocidade horizontal inicial :
Já a sua direção, é na horizontal, ou seja na componente :
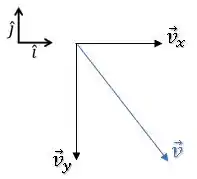
Já a velocidade na vertical, podemos calcular com a expressão de velocidade para um MUV:
Lembrando de que a aceleração é negativa no nosso referencial:
Substituindo , temos:
Passando o para dentro da raiz elevado ao quadrado, temos:
Agora, podemos escrever como vetor na direção :
Por fim, o vetor velocidade no momento em que ele atinge a água será:
Resposta
(a)
(b)
(c)