UFMG – Fundamentos de Mecânica – P1 – Questão P2.1
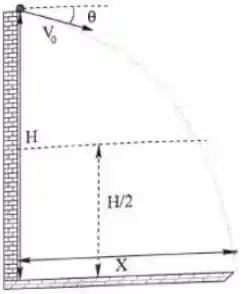
Uma bolinha de massa m é lançada de um muro, fazendo um ângulo com a horizontal para baixo, saindo do muro de uma altura H a partir do solo. Mede-se que a bolinha leva um tempo T para atingir o solo, a partir do instante que sai do muro. Dê suas respostas em função de e .
- Calcule a altura H do muro
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Queremos determinar a altura do muro, ou seja, queremos saber a posição inicial na qual a bolinha saiu.
Essa bolinha leva um tempo para atingir o chão, então é essa a informação chave que vamos usar!
Relembrando das equações de movimento para a componente (isso porque queremos saber , que está na direção vertical)
E ideia para resolver questões de cinemática é comparar os dados que temos com as equações
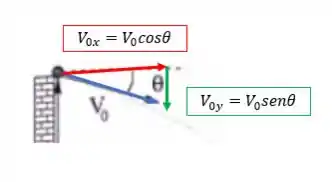
Isso sem esquecer que a velocidade inicial pode ser decomposta em componente vertical e horizontal
tranquilo até aqui?
Temos e e queremos saber , então através das equações de movimento vamos encontrar essa altura!
Vamos lá?
Passo 2
A partir da primeira equação temos a relação entre posição e tempo, e é essa equação que nos interessa!
Isso porque foi dado o tempo que a bolinha leva para, partindo da altura inicial , chegar até o chão
A aceleração da gravidade é conhecida (vale ) e a velocidade inicial da bolinha é a componente vertical da velocidade, e pelo desenho do passo anterior vemos que ela é negativa , o tempo e a posição já temos
Então agora é só substituir:
Beleza?
Passo 3
Agora é só isolar !
E é isso!
Espero ter ajudado!