Para bombardear um alvo, um avião em vôo horizontal a uma altitude de solta a bomba quando a sua distância horizontal até o alvo é de . Admite-se que a resistência do ar seja desprezível. Para atingir o mesmo alvo, se o avião voasse com a mesma velocidade, mas agora a uma altitude de apenas , ele teria que soltar a bomba a que distância horizontal do alvo?

Beleza, vamos lá! Ele fala que tem um avião que tá voando horizontalmente, ou seja a velocidade em y é zero, e esse avião tá voando a uma altura de , ou seja, e nesse caso, para acertar o alvo ele precisa soltar o míssil a , ou seja, de distância.

E a pergunta é qual a distância que temos que soltar o míssil se o avião estivesse voando a , ou seja,

Vamos desenhar o que tá acontecendo?

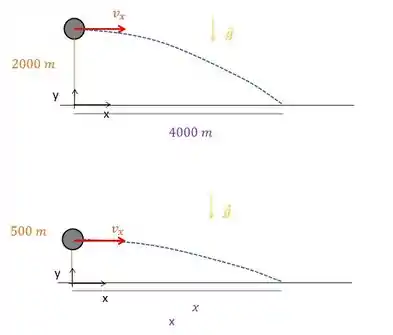
Beleza?

Já coloquei ali a aceleração da gravidade, apontando para baixo em relação ao eixo y. Ou seja, em y, temos um MUV. E em x, como não há aceleração, o movimento é uniforme.

Como a velocidade em x é a mesma nos dois casos, vamos descobrir ela! Pra isso, vamos analisar o primeiro caso, quando o avião tá a de altura. A posição em y varia de acordo com:

A posição final é zero, quando ele chega, a inicial é, como a velocidade é só horizontal, , e a aceleração em y vale:

O menos é porque aponta para baixo em relação ao eixo y.

Então:

Resolvendo isso daí, vemos que o tempo é

Maravilha, vamos olhar agora para o eixo x, que tem um movimento uniforme e ver qual é a sua velocidade, que é a mesma que ele vai ter quando o avião estiver a de altura.

A posição inicial em x é zero, a final é , e o tempo que ele demorou pra chegar lá foi de . Então:

Maravilha! Já sabemos a velocidade do míssil na horizontal!

Agora vamos analisar o segundo caso, quando o avião voa à de altura.