Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Limite com Mudança de Variável para Funções de Várias Variáveis

Ver Teoria
Exercício 101234567891112131415161718192021222324252627282930

Enunciado

  1. Decida, justificando, se existe ou não lim x , y → 0 ,   0 ⁡ x 2 ln ⁡ 3 x 2 + y 2 .
  2. Seja f a função dada por

f x , y = x 2 ln ⁡ 3 x 2 + y 2 arctg ⁡ 1 y 2 - x 2 .

Verifique se os limites abaixo existem e, em caso afirmativo, determine seu valor. Justifique.

b . 1 )   lim x , y → 0 ,   0 ⁡ f x , y b . 2 )   lim x , y → 1 ,   1 ⁡ f x , y

Passo 1

a)

Substituindo os valores x = 0 e y = 0 no limite caímos numa indeterminação “ 0 × - ∞ ”.

E parece difícil provar que esse limite não existe, porque independente do caminho de aproximação que usarmos, o termo dentro do l n vai tender a 0 + , e aí vai dar ruim.

Então vamos ter que achar algum jeito de sair dessa com o teorema do sanduíche/anulamento. Temos que manipular esse limite pra ele ficar melhor.

Isso costuma ser a parte mais difícil!

Passo 2

Vamos tentar achar uma expressão limitada. Vejamos nossa expressão: temos x 2 e, dentro do l n , o termo 3 x 2 + y 2 . Repare que:

0 ≤ x 2 ≤ 3 x 2 + y 2

Esse tipo de enquadramento costuma ser o ponto de partida pra calcular limites. Só que esse 3 x 2 + y 2 na direita não tá muito bom, então vamos dividir tudo por 3 x 2 + y 2 :

0 3 x 2 + y 2 ≤ x 2 3 x 2 + y 2 ≤ 3 x 2 + y 2 3 x 2 + y 2

0 ≤ x 2 3 x 2 + y 2 ≤ 1

Ok, agora temos algo limitado!

Passo 3

E como usamos isso pra calcular nosso limite? Vejamos... O limite é:

lim x , y → 0 ,   0 ⁡ x 2 ln ⁡ 3 x 2 + y 2

Concorda comigo que isso é igual a:

lim x , y → 0 ,   0 ⁡ x 2 ln ⁡ 3 x 2 + y 2 3 x 2 + y 2 3 x 2 + y 2

Ajeitando isso aí:

lim x , y → 0,0 ⁡ x 2 3 x 2 + y 2 3 x 2 + y 2 ln ⁡ 3 x 2 + y 2

Opaaa, agora ficou interessante!

Passo 4

A fração da esquerda x 2 3 x 2 + y 2 vimos que é limitada, agora vamos pra parte da direita.

Fazendo a substituição u = 3 x 2 + y 2 , temos

x , y → 0 ,   0   ⇒     3 x 2 + y 2 → 0   ⇒     u → 0

Correto? E isso significa que

lim x , y → 0,0 ⁡ 3 x 2 + y 2 ln ⁡ 3 x 2 + y 2 = lim u → 0 ⁡ u ln ⁡ u

Passo 5

Ainda temos uma indeterminação, então botamos o limite na forma:

lim u → 0 ⁡ ln ⁡ u 1 u

Agora temos uma indeterminação do tipo “ ∞ / ∞ ” e podemos aplicar a regra de l’Hôpital:

lim u → 0 ⁡ ln ⁡ u 1 u = lim u → 0 ⁡ 1 u - 1 u 2

O que dá:

lim u → 0 ⁡ - u 2 u = lim u → 0 ⁡ - u = 0

Portanto, isso significa que

lim x , y → 0,0 ⁡ 3 x 2 + y 2 ln ⁡ 3 x 2 + y 2 = 0

Passo 6

Recapitulando:

lim x , y → 0 ,   0 ⁡ x 2 ln ⁡ 3 x 2 + y 2 = lim x , y → 0,0 ⁡ x 2 3 x 2 + y 2 3 x 2 + y 2 ln ⁡ 3 x 2 + y 2

E vimos que:

  • x 2 3 x 2 + y 2 é limitado
  • lim x , y → 0,0 ⁡ 3 x 2 + y 2 ln ⁡ 3 x 2 + y 2 = 0

Logo, pelo teorema do anulamento:

lim x , y → 0 ,   0 ⁡ x 2 ln ⁡ 3 x 2 + y 2 = 0

Passo 7

b.1)

Conhecendo o gráfico da função a r c t g esse limite fica bem tranquilo de calcular. Quer dizer, na verdade você não precisa nem lembrar do gráfico, basta saber que

- π 2 < arctg ⁡ x < π 2

Botei x ali, mas poderia ser qualquer coisa. A questão é que podemos garantir que

- π 2 < arctg ⁡ 1 y 2 - x 2 < π 2

Eu falei do gráfico porque nele podemos ver que as retas y = - π 2 e y = π 2 são assíntotas horizontais:

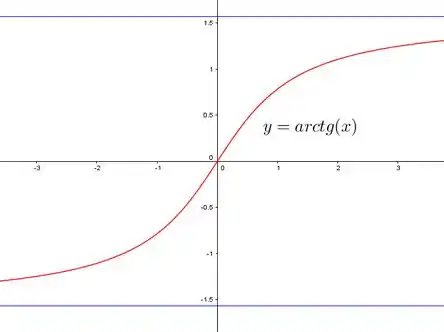
Passo 8

E quem adora expressão limitada é o teorema do anulamento né? Como vimos na letra a) que

lim x , y → 0 ,   0 ⁡ x 2 ln ⁡ 3 x 2 + y 2 = 0

Então temos

lim x , y → 0 ,   0 ⁡ x 2 ln ⁡ 3 x 2 + y 2 arctg ⁡ 1 y 2 - x 2 = 0

Passo 9

b.2)

Primeiramente, temos

lim x , y → 1 ,   1 ⁡ x 2 ln ⁡ 3 x 2 + y 2 = 1 . ln ⁡ 3 + 1 = ln ⁡ 4

Agora o problema vai ser calcular

lim x , y → 1 ,   1 ⁡ arctg ⁡ 1 y 2 - x 2

Isso porque substituindo x = y = 1 , temos uma indeterminação.

Passo 10

Agora o fato da função a r c t g ser limitada não adianta nada, porque não estamos mais multiplicando ela por algo tendendo a zero. Então nem dá mais pra aplicar o teorema do anulamento.

Por isso a boa vai ser tentar provar que o limite não existe.

Vamos por partes: primeiro vemos que

lim x , y → 1,1 ⁡ y 2 - x 2 = 0

Podemos, por exemplo, fixar x = 1 e testar os caminhos y → 1 - e y → 1 + . Assim temos os dois limites laterais

lim y → 1 - ⁡ y 2 - 1 = 0 - lim y → 1 + ⁡ y 2 - 1 = 0 +

Passo 11

Beleza, agora vamos passar pro limite

lim x , y → 1,1 ⁡ 1 y 2 - x 2

Com os nossos 2 caminhos vamos ter

lim y → 1 - ⁡ 1 y 2 - 1 = - ∞ lim y → 1 + ⁡ 1 y 2 - 1 = + ∞

Passo 12

Agora sim, vamos pro que interessa, que é o limite

lim x , y → 1,1 ⁡ arctg ⁡ 1 y 2 - x 2

Acabamos de ver que por um caminho o termo 1 y 2 - x 2 tende a - ∞ , e pelo outro ele tende a + ∞ . E temos (vide o gráfico da função a r c t g lá em cima):

lim x → - ∞ ⁡ arctg ⁡ x = - π 2 lim x → + ∞ ⁡ arctg ⁡ x = π 2

Passo 13

Voltando pro nosso limite todo,

lim x , y → 1,1 ⁡ x 2 ln ⁡ 3 x 2 + y 2 arctg ⁡ 1 y 2 - x 2

= ln ⁡ 4 lim x , y → 1,1 ⁡ arctg ⁡ 1 y 2 - x 2

Pelo caminho onde x = 1 e y → 1 - , isso dá - π 2 ln ⁡ 4 .

E pelo caminho onde x = 1 e y → 1 + , isso dá π 2 ln ⁡ 4 .

Por esses 2 caminhos obtemos 2 resultados diferentes, portanto o limite não existe.

Resposta

a) 0

b.1) 0

b.2) O limite não existe.

Exercícios de Livros Relacionados

29 – 36 Determine os valores máximo e mínimo absolutos de f no conjunto D.34 -fx ,y = x y 2 , D = x , yx ≥ 0 ,y ≥ 0 ,x 2 + y 2 ≤ 3 }
Calcular os limites seguintes:a) underset([[x - 1],[y - 2]])(lim) (e^(x y) - e^y + 1)
Calcular os limites seguintes:h) underset([[x - 1],[y - 2]])(lim) ln [(x y - 1)/(2 x y + 4)]
Calcular os seguintes limites de funções compostas:b) lim x → + ∞ y → + ∞ ⁡ e 1 x + y
Calcular os seguintes limites de funções compostas:d) lim x → 4 y → 2 ⁡ ln ⁡ x 2 + y 2 x - y + 1