Um tanque contém litros de água pura. Água salgada contendo de sal por litro entra no tanque a uma taxa de litros por minuto. A solução bem misturada é bombeada para fora do tanque na taxa de litros por minuto. Calcule qual a quantidade de sal após 5 minutos.
Passo 1
Vamos fazer um esquema pra deixar tudo que o enunciado deu bem claro na nossa cabeça:
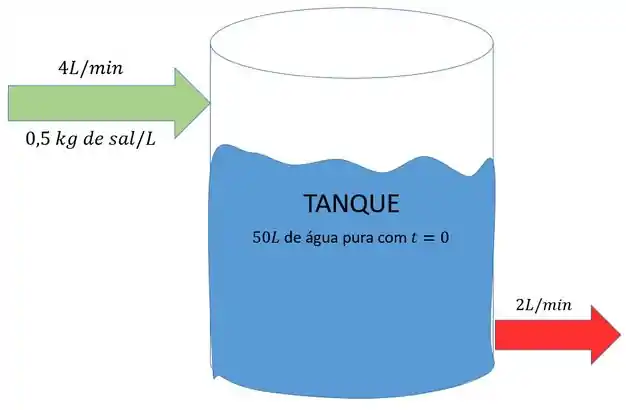
Pra facilitar, podemos também chamar a quantidade de sal no tanque após minutos de . Ou seja, temos que achar .
Beleza? Então vamos continuar!
Passo 2
Pra achar , vamos precisa da taxa de variação da quantidade de sal no tanque em função do tempo . E essa taxa de variação nada mais é que a taxa de entrada menos a taxa de saída !
Então vamos achar as taxas de entrada e de saída!
Passo 3
A taxa de entrada vai ser tranquila de achar!
O fluxo de entrada de água salgada é e tem de sal por litro. Então a taxa de entrada de sal é
Passo 4
Agora temos que tomar cuidado!
Enquanto a taxa de entrada de sal é fixa, a de saída depende do volume de água no tanque! E esse volume varia com o tempo, então podemos chamá-lo de .
Sabemos que e que a cada minuto entram litros de água e saem . Então, em relação ao volume, é como se entrassem .
Ou seja, o volume é . Escrevendo isso em função de :
Passo 5
Beleza, agora podemos calcular a taxa de saída de sal no tanque!
O fluxo de saída de água salgada é 2. E a concentração de sal nessa água é a quantidade de sal dividida pelo volume de água, certo? Então a taxa de saída de sal é essa concentração vezes o fluxo de saída! Ou seja:
Observação: um macete bom é pensar nas unidades: em , em e o fluxo de saída em . Os vão “cortar” e só vai sobrar !
Enfim, como temos
Passo 6
Show! Agora podemos achar a taxa de variação da quantidade de sal no tanque:
Passo 7
Vamos cair numa EDO linear de 1ª ordem:
A equação está na forma
com e .
Então vamos usar o fator integrante! Primeiro vamos calcular a integral
sem adicionar constante:
Então o nosso fator integrante é
Passo 8
Agora vamos calcular a integral
também sem adicionar constante:
Agora podemos encontrar a solução
sendo uma constante qualquer:
Passo 9
Pra determinar , vamos usar o fato que inicialmente não tem sal no tanque, ou seja :
Ótimo! Então
Passo 10
E isso tudo foi pra achar a quantidade de sal após minutos: