Um tanque contém inicialmente 10 litros de água pura. Injeta-se no tanque uma solução clorada à taxa de , contendo . A solução bem misturada é retirada do tanque à taxa de . A função que representa a quantidade de cloro após minutos é solução do problema com condição inicial:
(a)
(b)
(c)
(d)
(e)
Passo 1
Esse é um clássico problema de tanque! É sempre bom fazer um esquema pra visualizar melhor:
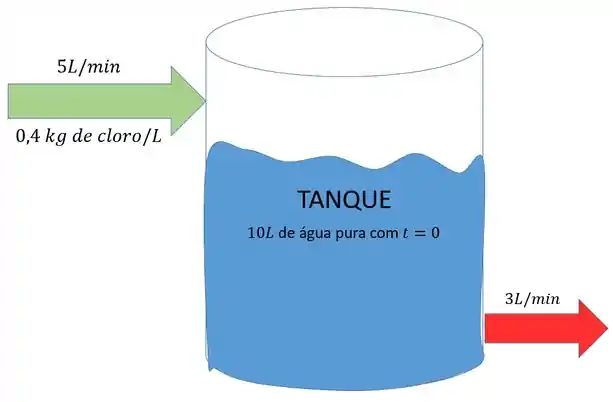
Passo 2
Primeiramente, podemos notar que com a água é pura, não há nenhum cloro.
Ou seja, .
Show, já eliminamos 2 opções!
Agora precisamos achar , a taxa de variação da quantidade de cloro no tanque em função do tempo. E a taxa de varição nada mais é do que quanto entra menos quanto sai, né?
Passo 3
Vamos focar primeiro na taxa de entrada. Temos de água clorada entrando a cada minuto e com de cloro em cada litro. Ou seja, temos de cloro entrando por minuto:
Passo 4
Atenção! Enquanto a taxa de entrada não depende do volume de líquido no tanque, a taxa de saída depende! Então vamos achar o volume em função do tempo . Sabemos que
Mas depois começa a entrar água clorada de um lado e sair do outro: entram e saem . Ou seja, pro volume de líquido no tanque, é como se estivessem entrando de água clorada! Temos iniciais mais a cada minuto!
Então o volume é
Passo 5
Beleza, agora podemos calcular a taxa de saída de cloro no tanque!
O fluxo de saída de água clorada é . E a concentração de cloro nessa água é a quantidade de cloro dividida pelo volume de água, certo? Então a taxa de saída de cloro é essa concentração vezes o fluxo de saída! Ou seja:
Observação: um macete bom é pensar nas unidades: em , em e o fluxo de saída em . Os vão “cortar” e só vai sobrar !
Enfim, como temos
Concluindo:
Resposta
Alternativa (a)