A dinâmica de uma partícula subatômica de massa pode ser estudada modelando-a confinada em um poço unidimensional de largura como mostra a figura.
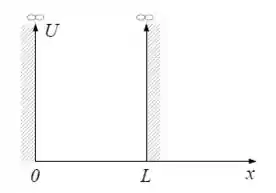
- Escreva a equação de Schrödinger para esta partícula com energia no poço.
- Obtenha, resolvendo a equação do item , as funções de onda normalizadas .
- Qual é a separação em energia entre os estados da partícula correspondentes aos dois níveis mais baixos de energia nesse poço?
Passo 1
Letra a)
A equação de Schrödinger é:
Porém, para a partícula no poço (), temos e a equação fica:
Podemos também rearrumá-la e mostrar ela de outra forma:
Passo 2
Letra b)
A equação da letra é:
Se definirmos uma nova constante:
Teremos:
Cuja solução é uma combinação de seno e coseno.
Passo 3
Agora, precisamos usar as condições de contorno na nossa função.
No caso de uma partícula na caixa, ela está completamente presa dentro da caixa, o que significa que a probabilidade dela ser encontrada fora da caixa é zero.
Pela continuidade da função de onda, isso nos dá as condições de contorno:
Como pela primeira condição, a segunda na verdade nos diz que:
Temos 3 opções para essa igualdade ser verdadeira:
- Igualamos . Neste caso, nossa função de onda é sempre zero, e não temos partícula nenhuma.
- Igualamos , fazendo . Neste caso, novamente nossa função de onda é sempre zero (pois zera o coseno ).
- Igualamos . Neste caso ficaríamos com , ( a gente recairia em )
A única opção viável é a terceira. Ela nos dá uma restrição no nosso .
A nossa função de onda fica:
Passo 4
Falta uma última coisa que o item nos pede, que é normalizar a função de onda.
Integrando ela de até , temos:
Pois fora do intervalo, a função é zero, então não contribui pra integral. Precisamos encontrar a constante para que essa equação seja satisfeita.
Resolvendo:
Pra resolver essa integral, é preciso uma dica dourada, que é:
Usando os limites de integração:
Porém:
As funções de onda normalizadas são:
Passo 5
Letra c)
Para achar a diferença de energia entre os dois níveis mais baixos do poço, precisamos saber a energia dos estados da partícula presa na caixa.
Para isso, basta igualarmos o que achamos pelas condições de contorno com a definição do nosso .
Ou, como , temos:
Os dois menores níveis de energia correspondem a e . Assim temos:
Resposta
Letra a)
Letra b)
Letra c)