Um elétron que está confinado em um poço de potencial infinito unidimensional de largura é excitado do estado fundamental para o primeiro estado excitado.
Essa excitação aumenta, diminui ou não tem nenhum efeito sobre a probabilidade de detectar o elétron em uma pequena região:
- No centro do poço?
- Perto de uma das bordas do poço?
Passo 1
Vamos resolver esse problema com argumentos mais qualitativos, lembrando que a função de onda para o elétron confinado é:
E a densidade de probabilidade de encontrar o elétron é:
A probabilidade de encontrar o elétron em uma região vai ser:
Obs: Você poderia tentar deduzir a fórmula exata da probabilidade e tentar comparar para os dois estados, mas essa análise seria bem mais complicada.
Passo 2
Letra a)
No estado fundamental, temos e a densidade de probabilidade fica:
O gráfico fica:
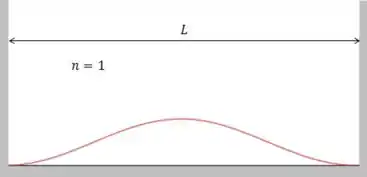
O primeiro estado excitado corresponde a .
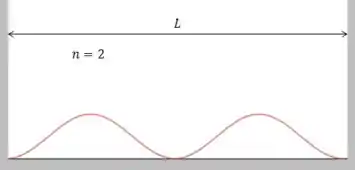
No primeiro gráfico é possível ver que está mais concentrado no centro da figura, enquanto na segunda o centro tem um mínimo.
Isso significa que a probabilidade de detectar o elétron numa pequena região ao redor do centro da figura diminui.
Passo 3
Letra b)
Usando os mesmos gráficos do item anterior, observa-se o seguinte:
Para , a função de onda é mais concentrada no meio da figura e próximo da parede ela é bem pequena, enquanto para temos dois máximos mais próximos das paredes, e a função de onda se concentra mais nesses dois máximos.
Como eles são mais próximos das paredes, cresce mais rápido próximo das paredes neste caso e por isso a probabilidade de achar o elétron em uma pequena região próxima da parede será maior.
Resposta
Letra a)
A probabilidade de encontrar o elétron em uma pequena região no centro do poço diminui.
Letra b)
A probabilidade de encontrar o elétron em uma pequena região próxima das paredes aumenta.