Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Probabilidade Conjunta de V.A. Bidimensionais Contínuas

Ver Teoria
Exercício 8123456791011121314151617181920212223242526272829303132

Enunciado

Probabilidade Conjunta

Considere a seguinte densidade conjunta

f x , y = 1 9 . e - y 3     ,     x > 0 , y > x

  1. Ache a densidade marginal de X .
  2. Ache a densidade marginal de Y .
  3. Calcule Pr ⁡ X > 1 Y < 4 .

Passo 1

( a )

Pra achar as marginais é só a gente aplicar a fórmula que a gente já tá cansado de usar ...

f x = ∫ 0 + ∞ f x , y   d y

= ∫ 0 + ∞ 1 9 . e - y 3   d y

= 1 9 . - 3 e - y 3 0 + ∞

= - 1 3 . 1 e ∞ - e 0

Como:

1 e ∞ = 0     e     e 0 = 1

Então:

= 1 3

Passo 2

( b )

Para a marginal de Y , é o contrário, a gente integra em x ...

f y = ∫ 0 y 1 9 . e - y 3     d x

Cuidado com o intervalo de x aí, ele é maior que zero, mas é menor que y ...

= 1 9 . e - y 3 . x 0 y

= y e - y 3 9

Passo 3

( c ) Antes de encontrarmos a probabilidade condicional, vamos dar uma olhada na região que ele quer? Seria essa área laranja aqui:

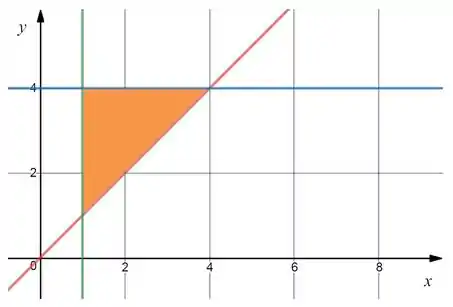
Essa é a região onde X > 1 , Y < 4 e Y > X ! Então isso aí é Pr ⁡ X > 1 ∩ Y < 4 . Pra fechar nossa condicional basta dividirmos isso por Pr ⁡ Y < 4 , que seria essa área aqui em baixo:

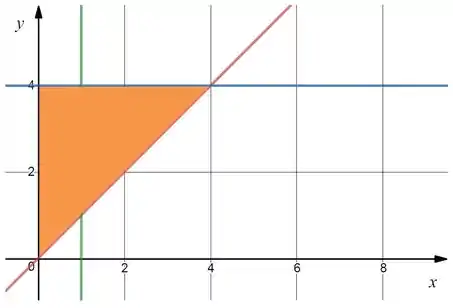
Show? Agora é só traduzirmos isso pras variáveis contínuas:

Pr ⁡ X > 1 Y < 4 = ∫ 1 4 ∫ x 4 1 9 . e - y 3 d y d x ∫ 0 4 y e - y 3 9 d y

Vamos resolver as integrais separadinhas!

Passo 4

∫ 1 4 ∫ x 4 1 9 . e - y 3 d y d x = ∫ 1 4 - 1 3 e - y 3 x 4 d x = ∫ 1 4 - 1 3 e - 4 3 + 1 3 e - x 3 d x =

= - 1 3 x e - 4 3 - e - x 3 1 4 = - 4 3 e - 4 3 - e - 4 3 + 1 3 e - 4 3 + e - 1 3 = e - 1 3 - 2 e - 4 3

Passo 5

∫ 0 4 y e - y 3 9 d y

Por partes:

∫ u d v = u v - ∫ v d u

u = y 3 ⇒ d u = 1 3

d v = e - y 3 3 ⇒ v = - e - y 3

∫ 0 4 y e - y 3 9 d y = - y e - y 3 3 0 4 + ∫ 0 4 e - y 3 3 d y = - 4 e - 4 3 3 - e - y 3 0 4 = - 4 e - 4 3 3 - e - 4 3 + 1 =

= 1 - 7 e - 4 3 3

Passo 6

Pra fechar:

Pr ⁡ X > 1 Y < 4 = e - 1 3 - 2 e - 4 3 1 - 7 e - 4 3 3 = 3 e - 1 3 - 6 e - 4 3 3 - 7 e - 4 3 = 3 e - 6 3 e 4 3 - 7

Resposta

a

1 3

b

y e - y 3 9

c

3 e - 6 3 e 4 3 - 7

Exercícios de Livros Relacionados

Suponha que duas variáveis aleatórias (X,Y) sejam uniformemente distribuídas num círculo de raio a. Então, a função de densidade de probabilidade conjunta é: f x , y = 1 π a 2 ,x 2 + y 2 ≤ a 2 f ( x ,
A distribuição de probabilidade conjunta é. Mostre que a correlação entre X e Y é zero, porém X e Y não são independentes.
Os pesos de tijolos de barro usadas em construção são distribuídas normalmente, com uma média de três libras e o desvio padrão de 0.25 libras. Suponha que os pesos dos tijolos sejam independentes e qu
Suponha que as variáveis aleatórias, existem uma função densidade de probabilidade conjunta. Determine o seguinte:
Suponha que é correlação entre X e Y seja P. Para as constantes a, b, c e d qual é a correlação entre as variáveis aleatórias