O valor da variável é um número no intervalo escolhido segundo uma densidade uniforme. De maneira similar, o valor da variável é um número no intervalo , escolhido segundo uma densidade uniforme. As variáveis são independentes. Um aluno toma os valores de obtidos em um experimento e desenha um triângulo retângulo, onde são os catetos. Qual a probabilidade que a hipotenusa desse triângulo seja menor que ?

Como vimos no passo queremos calcular , mas como vamos fazer isso? Será que temos que descobrir a densidade de ? Usar alguma propriedade de esperança condicional? Bem, vamos fazer essa questão de forma bem simples usando o domínio das nossas variáveis .

Colocando no plano cartesiano, temos que todos os possíveis valores para se encontram no quadrado unitário. E por serem uniformes e INDEPENDENTES, o par será uniforme no quadrado unitário.

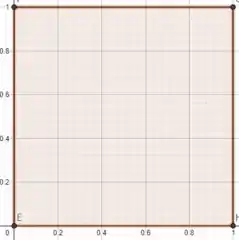
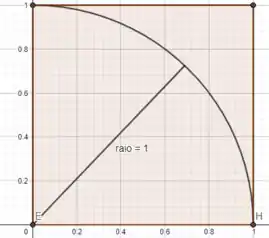
Os pontos de interesse, que satisfazem se encontram no quarto de circunferência.

Nós encontramos, no passo anterior, o conjunto dos pontos que satisfazem . e vimos que é um quarto de um círculo. Temos que a probabilidade desse conjunto será proporcional a sua área. Será a área total do quadrado dividida pela área do quarto de circulo, uma vez que é uniforme no quadrado unitário.

Então

Muitas vezes não precisamos trabalhar com a distribuição diretamente. Olhar nosso domínio pode ajudar muito.