UFSCAR. Cálculo 3. Lista de Estudos – Integrais Duplas. Questão 2.
2 – Calcular:
Em que é a região delimitada por , e .
Passo 1
Fala aí! Tudo belezinha por aí? Vamos resolver mais essa questão juntos? Vem comigo!
Bem, o problema pediu pra gente calcular essa integral, que é uma integral dupla
E disse que é pra gente fazer isso na região delimitada por , e . Mas o que isso quer dizer?
Bom, o primeiro passo será entender que região é essa, e para isso nós teremos que desenhá-la. Assim nenhum dado vai passar batido. Então bora fazer isso.
Passo 2
Nossa região de integração foi definida como sendo , e . Vamos começar desenhando essa primeira reta, a .
Para facilita a visualização vamos inverter essa função fazendo . Belezinha?
Agora vamos desenhar a reta
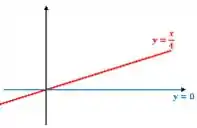
E também a reta
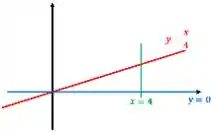
Ao fazer isso nós fechamos uma região que é a nossa região de integração:
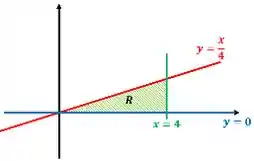
Perceba que se olharmos na direção do eixo , nossa região começa em e termina em , assim podemos perceber que . Já no eixo , nossa região começa na reta e termina na reta , assim podemos dizer que . E acabamos de obter nossos limites de integração.
Aqui vai uma dica muito importante, na hora de fazer a integração, fica muito mais tranquilo colocar a variável que está variando entre funções na integral de dentro, e a que está variando entre constantes na integral de fora.
Assim, nossa integral se tornará
Note que o intervalo da integral de fora está de acordo com e o da de dentro, com
Agora nossa preocupação é a de resolver essa integral. Então, bora lá!
Passo 3
Para resolver essa integral vamos utilizar o Teorema de Fubini, que diz que nós devemos fazer a integral de dentro, como se a de fora não existisse e depois, com o resultado da de dentro, fazer a integral de fora.
Olhando só para a integral de dentro, teremos:
Perceba que essa integral está em , então é visto como uma constante e pode ficar do lado de fora da integral
Essa integral é igual a
Agora vamos aplicar o princípio fundamental do cálculo substituindo os limites de integração na função que acabamos de encontrar. Lembrando que integramos e , então a substituição será só em . Ok?!
Show!!! E esse é o resultado da integral de dentro. Agora devemos fazer a integração de fora usando esse resultado como nossa função.
Passo 4
Devemos, então, integrar em relação a , substituindo o valor que encontramos no passo 3.
Podemos colocar o do lado de fora da integral, pois ele é uma constante.
E para resolver essa integral teremos que fazer uma substituição simples.
Fazendo
E a integral se torna
E a integral de é o próprio . Assim, ficamos com:
Voltando para a variável , nossa integral se torna
Maravilha!!! Agora basta aplicar os limites de integração, ficando com
E prontinho, encontramos o valor da nossa integral dupla.
Partiu próxima?!!!