UFSC, Araranguá, Cálculo B, P3 - 2022.2, Questão 1
Faça as mudanças de variáveis adequadas (transformação de coordenadas) e resolva a integral
Sendo a região limitada pelas retas , , e .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma integral dupla em uma região limitada por quatro retas e pediu pra gente resolver usando as mudanças de variáveis adequadas. Mas que mudanças seriam essas?
Bom, existe um teorema no cálculo que nos dá a relação:
Repare que é o Jacobiano, presente em qualquer mudança de variáveis, e é a nossa função escrita em termos de e .
Então, o que nós vamos fazer é encontrar um e , encontrar os novos limites de integração em função das novas variáveis, calcular o Jacobiano e substituir tudo na equação acima.
Vamos lá!
Passo 2
Nós temos a função . Vamos começar chamando:
Vamos resolver essas equações como um sistema, pra encontrar e . Dá primeira equação, temos:
Substituindo na segunda equação:
Isolando :
Substituindo em , temos:
Passo 3
Agora vamos encontrar nossos limites de integração. O enunciado nos disse que a região de integração é limitada pelas retas , , e . Plotando isso em um gráfico, fica assim:
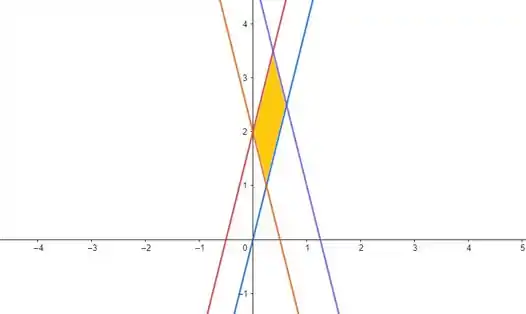
Repare que a nossa região é essa em amarelo. Essa região é limitada horizontalmente por e . Logo, varia no intervalo:
E ela é limitada verticalmente por e . Logo,
Mas esses intervalos precisam estar em termos de e . Então, vamos substituir os resultados que encontramos no passo anterior ( e ) para obter:
Passo 4
Agora só falta encontrar nossa . Pra isso vamos substituir e na equação:
Ah, não podemos esquecer do Jacobiano.
Pra calcular o Jacobiano, vamos fazer:
Calculando esse determinante, temos:
Ou
Passo 5
Agora podemos montar nossa integral:
Jogando a constante pra fora das duas integrais:
Vamos começar calculando a integral em :
Agora vamos calcular a integral em :
Prontinho, galera! Até a próxima! 😉