Esboce a região de integração e calcule as integrais a seguir
Passo 1
Eaew, belezinha?
O enunciado nos pede para calcularmos a seguinte integração
e também para esboçarmos a região de integração:
e .
Primeiro esboçar essa região e depois calcular a integral!
Passo 2
Para esboçar a região de integração da integral
olhamos para os limites de integração
e .
Ou seja, esboçamos os gráficos de e para :
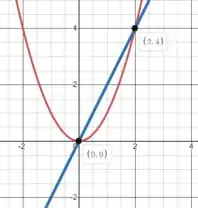
Passo 3
Agora vamos resolver as integrais, começando por , pois seus limites de integração dependem de :
Passo 4
Resolvendo a integral em :
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
.