James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 15 Seção 1 Problema 4.
(Cap 15.1 – Ex 4) (a) Estime o volume do sólido que está abaixo da superfície e acima do retângulo . Use a soma de Riemann com e escolha os pontos de amostragem como os cantos inferiores esquerdos.
(b) Use a Regra do Ponto Médio para estimar o volume do item (a).
Passo 1
E ai galerinha, show de bola?
Bora fazer mais uma?
Encostaa
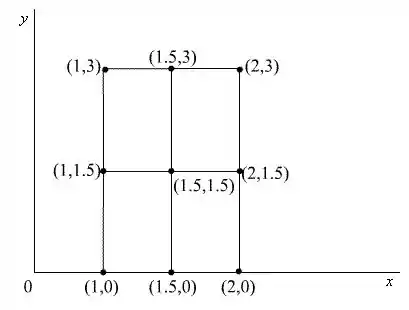
Iremos utilizar a soma de Riemann com sobre a região , para que possamos estimar o volume do sólido que se encontra abaixo da superfície e acima R. Os retângulos são mostrados na figura abaixo e a área de cada sub retângulo .
Os sub retângulos são mostrados na figura abaixo
Passo 2
- Então, obtemos
- Aproximando o volume usando a Regra do Ponto Médio com , calculamos nos centros de quatro retângulos mostrados na figura do passo 1. Logo . A área de cada sub – retângulo
Se , então o volume do sólido que está acima do retângulo R e abaixo da superfície é . Nós temos
Portanto
Pela imagem do passo 1, conseguimos obter os pontos de amostra nos cantos inferiores esquerdos como
Passo 3
Portanto, o volume do sólido é dado como:
Portanto, o volume do sólido é dado por .
Passo 4
Como mostrado na figura do passo 1, temos que nossos pontos médios do retângulo é
Passo 3
Então o volume do sólido e dado por
Portanto, o volume do sólido é dado por .
Resposta
- Portanto, o volume do sólido é dado por .
- Portanto, o volume do sólido é dado por .