UFSCAR, Sem Campus, Cálculo 3, Listas de C3 - Profª Alessandra Verri - Lista 3, Questão 3a
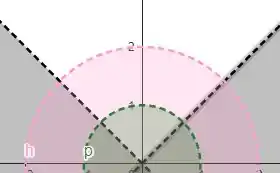
Esboce a região cuja área é dada pela integral
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos começar analisando a nossa integral:
A primeira parte importante é destacar aqui os intervalos de integração:
Além disso, importante lembrarmos como transformar as coordenadas polares:
Show, com essas informações, a gente vai conseguir calcular.
Passo 2
Vamos começar pelo intervalo do valor do raio.
Se a gente for analisar as coordenadas polares, vamos ter
Se somarmos cada componente elevada ao quadrado:
Pelos valores do raio
Reparem que temos duas circunferências. A região queremos é fica no intervalo entre elas:
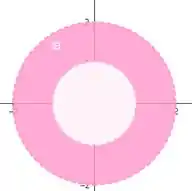
No caso, é a nossa região Rosa
Passo 3
Agora, vamos olhar para o intervalo de θ
Para ficar mais simples de enxergar, vamos trocar os valores por graus:
Juntando com a imagem anterior:
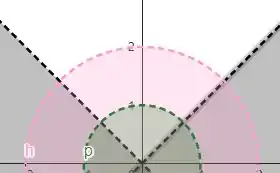
Resposta
