Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Região Retangular e Teorema de Fubini

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536

Enunciado

UFPE – Cálculo 2 – Listas Prof. Ricardo F. da Silva – Undecima lista – Questão 1e

Esboce a região de integração e calcule as integrais a seguir

e ) ∫ 0 π / 2 ∫ 0 cos ⁡ y x sin ⁡ y d x d y

Passo 1

Oi, tudo bem?

Vamos olhar com carinho essa integral aqui

∫ 0 π 2 ∫ 0 cos ⁡ y x sin ⁡ y d x d y

O problema pediu para esboçar a região e para calcular! Bom, você sabe por onde começar?

A ideia é começar olhando para a ordem de integração, no nosso caso

d x   d y

E analisar os limites de integração! O mais de dentro está relacionado com o x e o mais externo está relacionado com o y , assim

0 ≤ x ≤ cos ⁡ y

0 ≤ y ≤ π / 2

A ideia é retirar quatro equações (os extremos dos limites), esboçar todas juntas no mesmo gráfico e encontrar os pontos de encontro! E depois? Depois é #partiu integrar! Beleza?

Bora começar?

Passo 2

Nossos limites são

0 ≤ x ≤ cos ⁡ y

0 ≤ y ≤ π / 2

Tiramos daqui quatro equações

x = cos ⁡ y

x = 0

y = 0

x = π / 2

Então vamos esboçar essas quatro curvas! Ficamos com

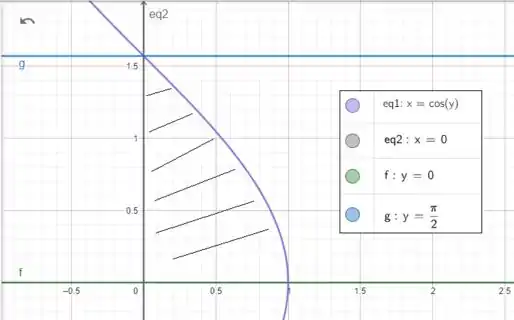
Nossa região é aquela que tem a curva x = cos ⁡ y sempre mais à direita e o eixo y mais à esquerda. E os limites em y vão de 0 até π 2

Tudo bem até aqui? Agora é #partiu integrar!

Passo 3

Integrando em x temos

∫ 0 π 2 ∫ 0 cos ⁡ y x sin ⁡ y d x d y = ∫ 0 π 2 x 2 2 0 cos ⁡ y sin ⁡ y d y = 1 2 ∫ 0 π 2 cos 2 ⁡ y sin ⁡ y d y

E por fim em y . Vamos chamar u = cos ⁡ y ,   d u = - sin ⁡ y d y

- 1 2 ∫ u 2 d u = - 1 2 u 3 3 = - 1 6 cos ⁡ y

E por fim aplicar os limites

= - 1 6 cos ⁡ π 2 + 1 6 cos ⁡ 0 = 1 6

Beleza? Espero ter ajudado!

Resposta

1 6

Exercícios de Livros Relacionados

Calcular underset(R)(∬) f (x , y) d x d y , onde:b) f (x , y) = y e^(x y) ; R é o retângulo (0 = x = 3)/(0 = y = 1)
Calcule a integral dupla. ∬ R s e n ( x + y ) d A ,R = x , y 0 ≤ x ≤ π 2 ,0 ≤ y ≤ π 2
Calcule a integral iterada. ∫ - 3 3 ∫ 0 π / 2 ( y + y 2 c o s x ) d x d y
Calcule a integral iterada. ∫ 0 1 ∫ 0 3 e x + 3 y d x d y
Utilize um sistema de computação algébrica para determinar o valor exato da integral ∬ Rx 5 y 3 e x y d A onde R = 0 ,1 × 0 ,1 . Em seguida, use o SCA para desenhar o sólido cujo volume é dado pela in