Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Resistência e Resistividade

Ver Teoria
Exercício 28123456789101112131415161718192021222324252627293031323334353637383940414243444546474849505152535455565758

Enunciado

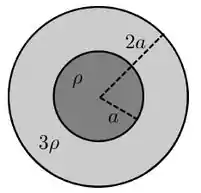
Um fio condutor retilíneo de comprimento L tem a seção transversal mostrada na figura abaixo. Ele é formado por um cilindro condutor de raio a e resistividade ρ cercado por uma casca condutora cilíndrica de raio interno a , raio externo 2 a e resistividade 3 ρ . Se uma corrente flui paralelamente ao eixo deste fio e o campo elétrico é constante em seu interior, podemos afirmar que a resistência elétrica deste fio vale:

(a) ρ L 2 π a 2

(b) 2 ρ L π a 2

(c)   ρ L 4 π a 2

(d) 4 ρ L π a 2

(e) ρ L 3 π a 2

(f) 3 ρ L π a 2

(g) ρ L π a 2

Passo 1

Nesse exercício a gente pode tratar o fio da imagem como se fossem dois resistores em paralelo. Ta mas como assim?

O cilindro condutor de raio a vai ser um resistor em paralelo com outro resistor que é a casca cilíndrica deu pra entender?

Aí a gente vai calcular a resistência de cada um deles e fazer a associação em paralelo, que é

1 R = 1 R 1 + 1 R 2

Passo 2

A resistência do cilindro condutor vai ser

R d e n t r o = ρ L π a 2

Enquanto a resistência da casca cilíndrica vai ser

R f o r a = 3 ρ L 3 π a 2 = ρ L π a 2

Logo

1 R = 1 ρ L π a 2 + 1 ρ L π a 2

1 R = 2 π a 2 ρ L

R = ρ L 2 π a 2

Logo, a alternativa correta é a letra A :)

Resposta

(a) ρ L 2 π a 2

Exercícios de Livros Relacionados

Uma barra de alumínio de seção reta quadrada tem 1,3 m de comprimento e 5,2 m m de lado. (a) Qual é a resistência entre as extremidades da barra? (b) Qual deve ser o diâmetro de uma barra cilíndrica d
Os enrolamentos de cobre de um motor têm uma resistência de 50 Ω a 20 º C º quando o motor está frio . Depois de o motor trabalhar durante várias horas, a resistência aumenta para 58 Ω . Qual é a nova
Quando um fio de metal é aquecido, não é apenas a resistividade que muda; o comprimento e a área do fio também são afetados. De acordo com a equação R=ρ L / A , as três grandezas devem ser levadas em
Se o número que indica o calibre de um fio aumenta de 6, o diâmetro é dividido por 2; se o calibre aumenta de 1, o diâmetro é dividido por 2 1 / 6 (veja a tabela do Problema 4). Com base nessas inform
Na Fig. 26-29, uma corrente elétrica atravessa um tronco de cone circular reto de resistividade 731 Ω · m , raio menor a = 2,00 m m , raio maior b = 2,30 m m e comprimento L = 1,94 c m . A densidade d